物事を体系的に整理し、そこから得た情報を根拠として、矛盾なく考える。それが論理的思考です。
英語では「ロジカル・シンキング」と呼ばれます。
前回に続き「ロジカル・シンキング」を鍛える問題を3問出します。難しい問題を出題したので時間を取って解いてみてください。
まずは初級の問題を解きたい方はこちらをご覧ください!
問1.10回のじゃんけん
A、Bの2人が、じゃんけんで10回勝負をした。
Aはグーを3回、チョキを6回、パーを1回だした。
Bはグーを2回、チョキを4回、パーを4回だした。

あいこは一度もならなかった。
熱中しすぎた2人は何の手をどの順番でだしたか覚えていない。
多く勝ったのはどっち?
解説
何から考えていけばいいのか、とっかかりすら見えませんが、そこに気づけるかが、この問題の最大のポイントです。
問題文に書かれていないヒントを読み解く
この問題のポイントは、「隠れたヒント」を見つけることです。
それが見つかるのは、この部分。
“あいこには一度もならなかった。”
ここから、ひとつの法則が導き出されます。
それは、相手に必ず、自分がだした手とは違う手を出しているという事実です。つまり、
Aがグーをだしたとき、Bはかならずチョキかパーを出している。
Aがチョキをだしたとき、Bはかならずグーかパーを出している。
Aがパーをだしたとき、Bはかならずグーかチョキを出している。
ということです。
「手をだした回数」に注目
Aがだした手に対して、Bがだした可能性のある手が分かりました。 たとえばAがグーをだした時、Bはチョキかパーをだしています。 つまるところAがグーをだした3回のうち、Bは 「3回ともチョキ」 「1回はチョキで、2回はパー」 「2回はチョキで、1回はパー」 「3回ともパー」 の可能性が考えられます。 でもひとつずつパターンを検証していくのはかなり大変です。。。。 そこで、Bのだした手が特定できなくても、勝敗が特定できる組み合合わせに直目すればよいのです。 それは、Aがだした手と、Bが「出したと思われる手」の回数が同じ時です。 Aがチョキを出した回数と、Bが出したグーとパーの合計数はどちらも6回。つまりAが6回チョキを出したとき、Bがグーを2回、パーを4回出していたと確定します。 よってAがチョキをだした6回の戦績はAの4勝2敗ということが分かります。
おのずとわかる対戦結果
これでBがグーかパーを出した時の勝敗は全て分かりました。
そして残りの勝負でBが出したのは「チョッキ4回」というのもわかっています。
それに対しAはグーを3回、パーを1回出しています。
つまり、残り4回の戦績はAの3勝1敗になります。
よって、最終的にはAが7勝3敗で勝ちました。
回答
多く勝ったのは”A”
Point
- いっけん手掛かりにはならにあ情報も、「そこからさらにわかること」を考えてみると、解決のとっかかりが見えてくる
問2.複雑な一週間
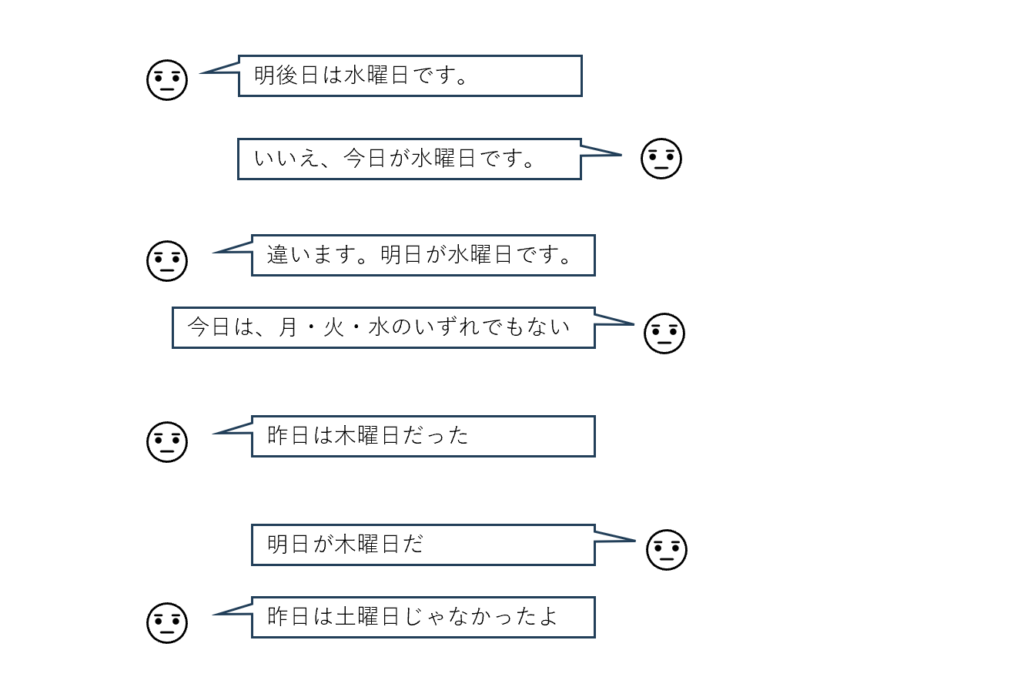
7人のうち、真実を語っているのは1人だけ。
今日は何曜日?
解説
バラバラな情報をもとに考えるときは、まず何をするべきか。難易度自体は高くありませんので、冷静に論理的に紐解いていきましょう。
まずは基準を整える
発言の内容がバラバラで、考えるのも嫌になってしまいます。
こういった、基準や表現がバラバラな情報について考える場合は、
まずは基準を整えていきましょう。
・明後日は水曜日
・今日が水曜日
・明日が水曜日
・今日は月・火・水ではない
・昨日は木曜日
・明日は木曜日
・昨日は土曜日ではない
問題で問われているのは「今日の曜日」です。
そこで、この7人の発言を、「今日」を基準にした形式に書き換えてみます。
・今日は月曜日
・今日は水曜日
・今日は火曜日
・今日は木・金・土・日のいずれか
・今日は金曜日
・今日は水曜日
・今日は月・火・水・木・金・土のいずれか
新たな手がかりを導く
基準を整えたことで、7人の発言において、ほとんどの曜日が2回以上登場していることが分かりました。 しかし、7人のうち本当のことを言っているのは1人だけ。 例えば「今日は月曜日」が正解だとした場合、AもGも正しいことを言っているということになり、「真実を語っているのは1人」という問題文と矛盾してしまいます。
つまり2人以上が示している曜日ではないということです。
7人の「今日が何曜日か」という発言で1回のみ登場する曜日が正解だとわかります! それは日曜日です。
回答
今日は”日曜日”
Point
- 分かっている情報の性質がバラバラな時は、まずは同じ基準に揃えられないかを考える
問3.書道コンテストの参加数
書道のレベルを競う社会人の全国大会が行われた。
1社につき必ず3人の社員が参加している。
あなたの会社からはA、B、Cの3人が出場したところ、次のような結果になった。
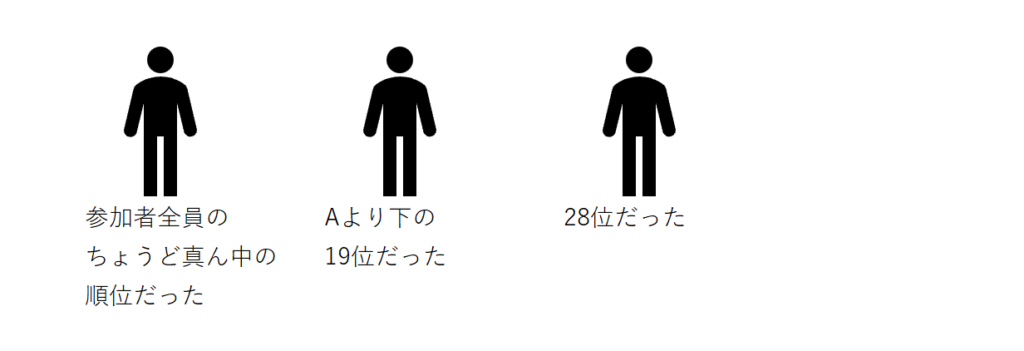
いくつの企業が、大会に参加したのだろうか?
解説
与えられている情報が少なく断片的のため、解けないのではないか?と思えます。しかし分かっている情報を、ひとつずつじっくり考えていくと、次第に道が開けていきます。
与えられた情報を「別角度」で眺める
解決の糸口が見えない時は「10回のじゃんけん」のように、事実の見方を変えることで別の情報を得られないか考えてみましょう。 まずはAの結果から見ていきます。 Aは「参加者全員のちょうど真ん中の順位」でした。ここから分かることは、「真ん中の順位」が存在したということです。 つまり、大会に参加した人数は奇数であることが分かりました。 参加者が5人→真ん中の順位は3位 参加者が6人→真ん中の順位は存在しない 加えて、各企業から出場している社員は3人。 すなわち参加者の人数は「奇数かつ3の倍数」を満たす数です。
Bの順位から分かること
次に、Bの結果に注目します。 Bは「Aより下の19位」でした。 これは、「ちょうど真ん中の順位(Aの順位)」が、19位より上になくてはいけないということを意味します。 ただし、Aが18位が真ん中だとすると参加総数は35人になりますが、これは「3の倍数」ではないため、「各企業から3人ずつ参加している」という状況と矛盾するためです。 つまり、考えられるAの順位として最も大きいのは17位。 よって、参加者としてありえる最大数は33人です。 これは先ほど判明した「奇数かつ3の倍数」の条件に当てはまります。 反対に、参加者としてありえる最小数は21人です。 Bが19位のため、少なくとも19よりは多い「3の倍数」の人数が参加していることは確実だからです。
Cの順位から分かること
最後に、Cの順位を見てみます。Cは「28位」でした。 全参加者は「奇数勝つ3の倍数(3,9,・・・,27,33,39)」の人数と分かっているため、参加者が28人という可能性はあり得ません。 28より大きくて、条件に当てはまる最小の数は33。 ということで、少なくとも33人以上の参加者がいるとわかります。 先ほどの「参加者としてありえる最大数は33人」という事実と組み合わせると、条件を満たすのは「参加者数が33人」の場合のみです。 そして、各社から3人が参加している。 よって参加企業は11社です。
回答
参加したのは”11社”
Point
- たとえ分かっている情報が少なくても、すべての言葉を別角度から眺めて、そこから分かる別の真実を導いていく
まとめ
前回の問題より難易度が高いですが、解けたでしょうか?もし全問正解できていたらあなたはロジカルシンキングをマスターしたも同然です!その知識をみんなに連携しましょう!
IT転職を成功させたい方へ(登録無料)

IT転職では、転職エージェントを使うかどうかで結果が大きく変わります。

実際、IT業界で200名以上の面接を担当していますが、 転職エージェントを利用している方は内定率が明らかに高いです。
以下では、現役人事の視点から本当におすすめできるIT転職エージェントを紹介します。
おすすめエージェント比較表
| サービス名 | 強み・特徴 | 対象者 | おすすめ度 |
|---|---|---|---|
| テックゴー | 年収UP・回数無制限の面接対策 | 経験者(2年〜) | |
| リクルートエージェント | 圧倒的な求人数・非公開案件 | 全員 | |
| 第二新卒エージェントneo | 書類通過率94%・20代特化 | 若手・既卒 | |
| UZUZ既卒 | ブラック企業排除・未経験からIT | 未経験・既卒 |
🏆 まず登録すべきおすすめエージェント
テックゴー | IT転職専門【おすすめNo.1】

実務経験2年以上のエンジニア向け。年収アップに特化したIT転職エージェント。
登録は30秒・完全無料。情報収集だけでもOKです。
※登録後も無理な応募を勧められることはありません
※完全無料・登録30秒
その他のおすすめエージェント
リクルートエージェント | 求人数No.1

ITエンジニア専門のキャリアアドバイザーが在籍し、書類添削・面接対策などのサポート体制が手厚いのが特徴の国内大手のエージェント。
第二新卒エージェントneo | 20代特化

20代(18〜29歳)の第二新卒・既卒・フリーター専門で、書類通過率94.7%・Googleクチコミ★4.4の高評価を誇る転職エージェント。
UZUZ既卒 | 未経験・既卒向け

第二新卒や既卒、フリーター、ニートなどの20代に特化した転職エージェント。

転職エージェントはすべて無料で利用できます。
複数登録して比較することで、より条件の良い求人に出会える可能性が高まります。
特にテックゴーは面接対策が回数無制限のため、 IT転職を成功させたい方は必ず登録しておくことをおすすめします。
まずは無料登録して、どんな求人があるか確認してみてください。





コメント