※本記事はプロモーションを含みます。
「エクセルにエンジニアリング関数ってあるけど、全部で何個?」
「どういう時に使えばいいの?」
この記事では、エクセルOffice 365で使えるエンジニアリング関数全54種類すべてについて、「どんな関数なのか」「どうやって使うのか」を、解説します。
- エンジニアリング関数って全部で何個あるか?
- どんな時に、どう使うのか?
エクセル「エンジニアリング関数」とは?
主に工学的な計算や、数値を異なる基数(進数)間で変換するための関数
普通の四則演算や統計関数とは異なり、特に以下の分野で使用します。
- 複素数 (Complex Number) の計算:
i (虚数単位) を含む複雑な計算をエクセルで扱えます。 - 数体系(基数)の変換:
10進数、2進数、16進数、8進数といった進数間の変換を簡単に行えます。 - ベッセル関数や誤差関数:
物理学や信号処理などの分野で使われる特殊な関数の計算ができます。
エンジニアリング関数全54種類の一覧表

まずは、Office 365で使えるエンジニアリング関数全54種類を一覧で確認してみましょう。
| 関数の種類 | 関数名 | 構文 | 関数の意味 |
| ビット演算 | BITAND | BITAND(数値1, 数値2) | 2つの数値のビット単位の AND 演算の結果を返します。 |
| BITLSHIFT | BITLSHIFT(数値, シフト量) | 数値を指定したビット数だけ左にシフトします。 | |
| BITOR | BITOR(数値1, 数値2) | 2つの数値のビット単位の OR 演算の結果を返します。 | |
| BITRSHIFT | BITRSHIFT(数値, シフト量) | 数値を指定したビット数だけ右にシフトします。 | |
| BITXOR | BITXOR(数値1, 数値2) | 2つの数値のビット単位の XOR 演算の結果を返します。 | |
| 進数変換 | BIN2DEC | BIN2DEC(数値) | 2進数を10進数に変換します。 |
| BIN2HEX | BIN2HEX(数値, [桁数]) | 2進数を16進数に変換します。 | |
| BIN2OCT | BIN2OCT(数値, [桁数]) | 2進数を8進数に変換します。 | |
| DEC2BIN | DEC2BIN(数値, [桁数]) | 10進数を2進数に変換します。 | |
| DEC2HEX | DEC2HEX(数値, [桁数]) | 10進数を16進数に変換します。 | |
| DEC2OCT | DEC2OCT(数値, [桁数]) | 10進数を8進数に変換します。 | |
| HEX2BIN | HEX2BIN(数値, [桁数]) | 16進数を2進数に変換します。 | |
| HEX2DEC | HEX2DEC(数値) | 16進数を10進数に変換します。 | |
| HEX2OCT | HEX2OCT(数値, [桁数]) | 16進数を8進数に変換します。 | |
| OCT2BIN | OCT2BIN(数値, [桁数]) | 8進数を2進数に変換します。 | |
| OCT2DEC | OCT2DEC(数値) | 8進数を10進数に変換します。 | |
| OCT2HEX | OCT2HEX(数値, [桁数]) | 8進数を16進数に変換します。 | |
| 複素数 | COMPLEX | COMPLEX(実数部, 虚数部, [接尾辞]) | 実数部と虚数部から複素数を作成します。 |
| IMABS | IMABS(複素数) | 複素数の絶対値(モジュラス)を返します。 | |
| IMAGINARY | IMAGINARY(複素数) | 複素数の虚数係数を返します。 | |
| IMARGUMENT | IMARGUMENT(複素数) | 複素数の偏角(角度)を返します。 | |
| IMCONJUGATE | IMCONJUGATE(複素数) | 複素数の共役複素数を返します。 | |
| IMCOS | IMCOS(複素数) | 複素数のコサインを返します。 | |
| IMCOSH | IMCOSH(複素数) | 複素数のハイパーボリックコサインを返します。 | |
| IMCOT | IMCOT(複素数) | 複素数のコタンジェントを返します。 | |
| IMCSC | IMCSC(複素数) | 複素数のコセカントを返します。 | |
| IMCSCH | IMCSCH(複素数) | 複素数のハイパーボリックコセカントを返します。 | |
| IMDIV | IMDIV(複素数1, 複素数2) | 2つの複素数の商(割り算)を返します。 | |
| IMEXP | IMEXP(複素数) | 複素数の指数(eの複素数乗)を返します。 | |
| IMLN | IMLN(複素数) | 複素数の自然対数(eを底とする)を返します。 | |
| IMLOG10 | IMLOG10(複素数) | 複素数の10を底とする対数を返します。 | |
| IMLOG2 | IMLOG2(複素数) | 複素数の2を底とする対数を返します。 | |
| IMPOWER | IMPOWER(複素数, 累乗) | 複素数の指定した累乗を返します。 | |
| IMPRODUCT | IMPRODUCT(複素数1, [複素数2], …) | 複素数の積(掛け算)を返します。 | |
| IMREAL | IMREAL(複素数) | 複素数の実数係数を返します。 | |
| IMSEC | IMSEC(複素数) | 複素数のセカントを返します。 | |
| IMSECH | IMSECH(複素数) | 複素数のハイパーボリックセカントを返します。 | |
| IMSIN | IMSIN(複素数) | 複素数のサインを返します。 | |
| IMSINH | IMSINH(複素数) | 複素数のハイパーボリックサインを返します。 | |
| IMSQRT | IMSQRT(複素数) | 複素数の平方根を返します。 | |
| IMSUB | IMSUB(複素数1, 複素数2) | 2つの複素数の差(引き算)を返します。 | |
| IMSUM | IMSUM(複素数1, [複素数2], …) | 複素数の和(足し算)を返します。 | |
| IMTAN | IMTAN(複素数) | 複素数のタンジェントを返します。 | |
| ベッセル関数 | BESSELI | BESSELI(X, 順序) | 変形ベッセル関数 I (第1種) を返します。 |
| BESSELJ | BESSELJ(X, 順序) | ベッセル関数 J (第1種) を返します。 | |
| BESSELK | BESSELK(X, 順序) | 変形ベッセル関数 K (第2種) を返します。 | |
| BESSELY | BESSELY(X, 順序) | ベッセル関数 Y (第2種) を返します。 | |
| 誤差関数 | ERF | ERF(下限, [上限]) | 誤差関数 (Gauss error function) を返します。 |
| ERF.PRECISE | ERF.PRECISE(下限, [上限]) | 誤差関数 (より高精度なバージョン) を返します。 | |
| ERFC | ERFC(下限) | 相補誤差関数を返します。 | |
| ERFC.PRECISE | ERFC.PRECISE(下限) | 相補誤差関数 (より高精度なバージョン) を返します。 | |
| その他 | CONVERT | CONVERT(数値, 換算前単位, 換算後単位) | 異なる単位間で数値を変換します。 |
| DELTA | DELTA(数値1, [数値2]) | 2つの値が等しいかどうかを判定するクロネッカーのデルタを返します。 | |
| GESTEP | GESTEP(数値, [ステップ]) | 数値がステップ値以上であるかどうかを判定するヘヴィサイドの階段関数を返します。 |
【種類別】エンジニアリング関数の詳しい使い方と使用例

ここからは、上で分類した関数の種類ごとに、各関数を詳しく見ていきましょう!
ビット演算に関する関数(5種類)
ビット演算は、数値を2進数として扱い、ビットレベルで操作を行う計算です。
プログラミングや低レベルなデータ処理で役立ちます。
BITAND:ビット単位のAND
ビット単位の AND 演算の結果を返します。
関数の意味
数値1と数値2を2進数に変換し、両方のビットが「1」のときだけ結果のビットを「1」にします。
構文
BITAND(数値1, 数値2)
関数の使用例
保有権限5と、チェックしたい権限1を入力する場合
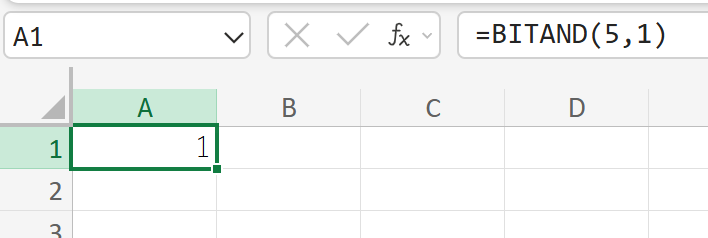
複数のフラグが設定された数値の中から、特定のフラグが立っているか(権限を持っているか)を判別するのに利用できます。
BITLSHIFT:ビット単位の左シフト
数値を指定したビット数だけ左にシフトします。
関数の意味
数値の2進数表現を左にずらします。左に1シフトすると、元の値に2を掛けたのと同じ結果になります。
構文
BITLSHIFT(数値, シフト量)
関数の使用例
数値10、シフト量3の10進数はいくつか?
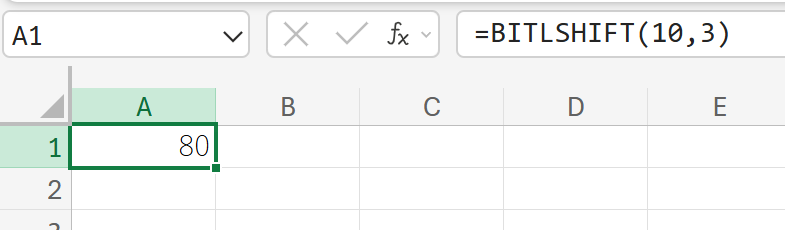
BITOR:ビット単位のOR
ビット単位の OR 演算の結果を返します。
関数の意味
数値1と数値2を2進数に変換し、どちらか一方、または両方のビットが「1」のとき、結果のビットを「1」にします。
構文
BITOR(数値1, 数値2)
関数の使用例
表の数字を用いてBITOR関数を使用し、結果の10進数を求めなさい。
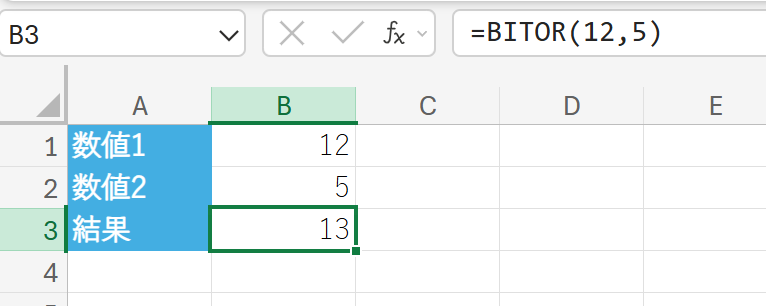
BITRSHIFT:ビット単位の右シフト
数値を指定したビット数だけ右にシフトします。
関数の意味
数値の2進数表現を右にずらします。右に1シフトすると、元の値から2を割ったのと同じ結果(小数点以下切り捨て)になります。
構文
BITRSHIFT(数値, シフト量)
関数の使用例
以下の条件でBITRSHIFT関数を使用し、結果の10進数を求めなさい。
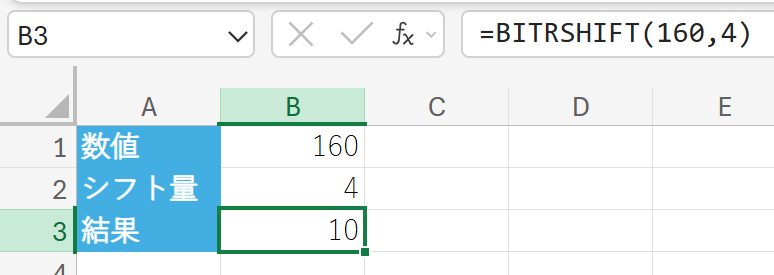
BITXOR:ビット単位の排他的OR (XOR)
ビット単位の XOR 演算の結果を返します。
関数の意味
数値1と数値2を2進数に変換し、どちらか一方だけのビットが「1」のとき、結果のビットを「1」にします(両方1、または両方0の場合は0)。
構文
BITXOR(数値1, 数値2)
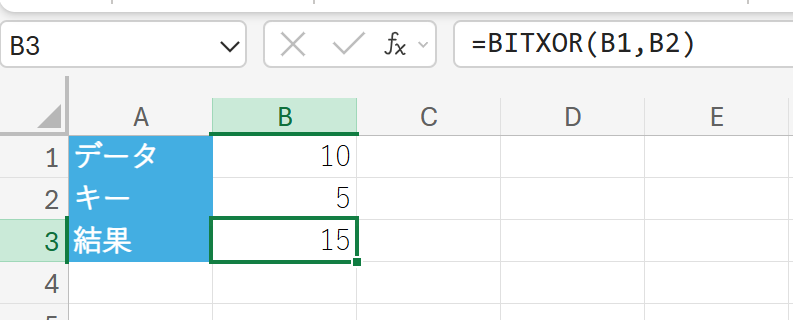
関数の使用例
以下の数値を用いて、データをキーで暗号化し、さらにその暗号化されたデータを同じキーで復号化するプロセスを考えます。
キー(暗号化に使う値): 5
データ(元の値): 10
数体系(進数)変換に関する関数(12種類)
これらの関数は、10進数(DEC)、2進数(BIN)、8進数(OCT)、16進数(HEX)間で数値を相互に変換するために使われます。システム開発やデータ通信の分野で特に役立ちます。
BIN2DEC:2進数を10進数に変換
関数の意味2進数(バイナリ)で表された数値を、私たちが日常使う10進数に変換します。
構文
BIN2DEC(数値)
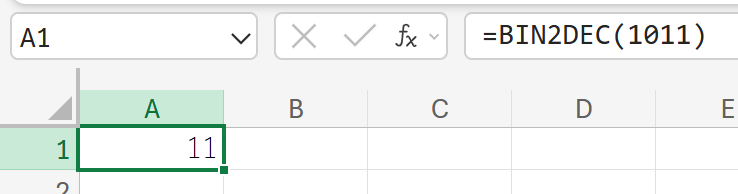
関数の使用例
1011(2進数表記)のデータを、通常の10進数に変換しなさい。
BIN2HEX:2進数を16進数に変換
関数の意味
2進数を16進数(ヘキサ)に変換します。変換後の桁数を指定できます。
構文
BIN2HEX(数値, [桁数])
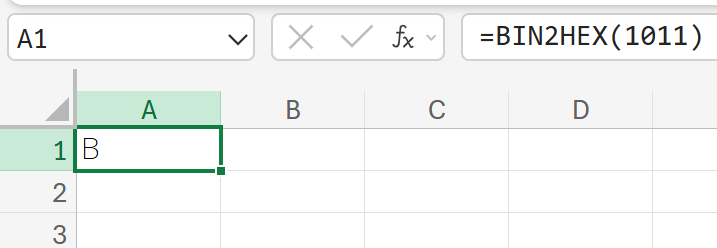
関数の使用例
1011(2進数表記)のデータを、16進数に変換しなさい。
BIN2OCT:2進数を8進数に変換
関数の意味
2進数を8進数(オクタル)に変換します。変換後の桁数を指定できます。
構文
BIN2OCT(数値, [桁数])
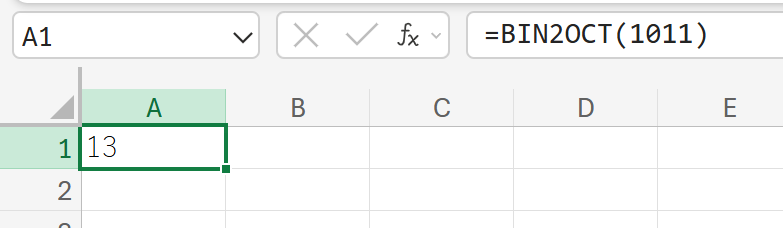
関数の使用例
1011(2進数表記)のデータを、8進数に変換しなさい。
DEC2BIN:10進数を2進数に変換
関数の意味
10進数を2進数(バイナリ)に変換します。変換後の桁数を指定できます。
構文
DEC2BIN(数値, [桁数])
関数の使用例
13を、2進数に変換しなさい。
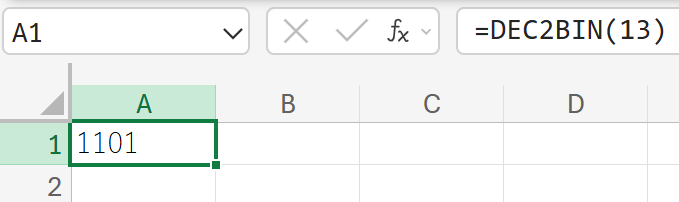
DEC2HEX:10進数を16進数に変換
関数の意味
10進数を16進数(ヘキサ)に変換します。変換後の桁数を指定できます。
構文
DEC2HEX(数値, [桁数])
関数の使用例
13を、16進数に変換しなさい。
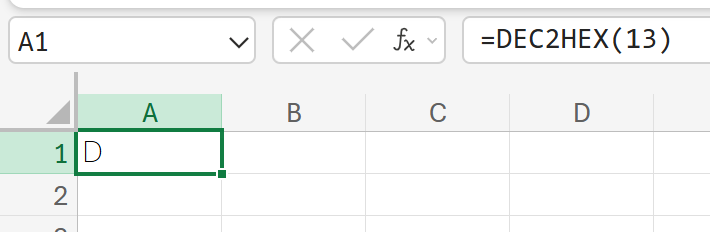
DEC2OCT:10進数を8進数に変換
関数の意味
10進数を8進数(オクタル)に変換します。変換後の桁数を指定できます。
構文
DEC2OCT(数値, [桁数])
関数の使用例
13を、8進数に変換しなさい。
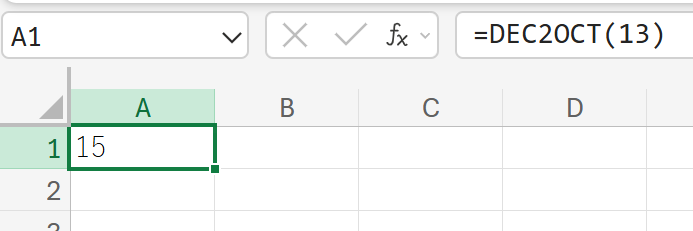
HEX2BIN:16進数を2進数に変換
関数の意味
16進数を2進数に変換します。変換後の桁数を指定できます。
構文
HEX2BIN(数値, [桁数])
関数の使用例
1A(16進数表記)のデータを、2進数に変換しなさい。
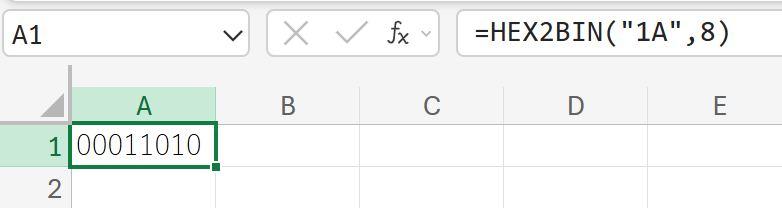
HEX2DEC:16進数を10進数に変換
関数の意味
16進数を10進数に変換します。
構文
HEX2DEC(数値)
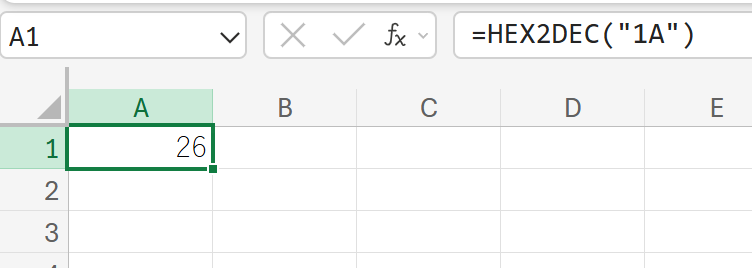
関数の使用例
1A(16進数表記)のデータを、10進数に変換しなさい。
HEX2OCT:16進数を8進数に変換
関数の意味
16進数を8進数に変換します。変換後の桁数を指定できます。
構文
HEX2OCT(数値, [桁数])
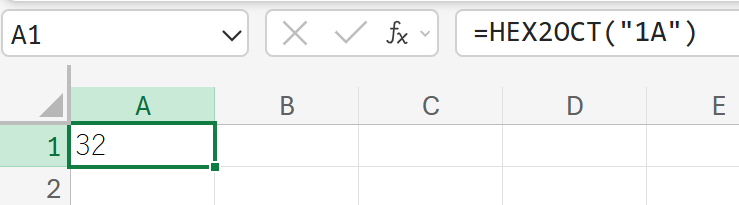
関数の使用例
1A(16進数表記)のデータを、8進数に変換しなさい。
OCT2BIN:8進数を2進数に変換
関数の意味
8進数を2進数に変換します。変換後の桁数を指定できます。
構文
OCT2BIN(数値, [桁数])
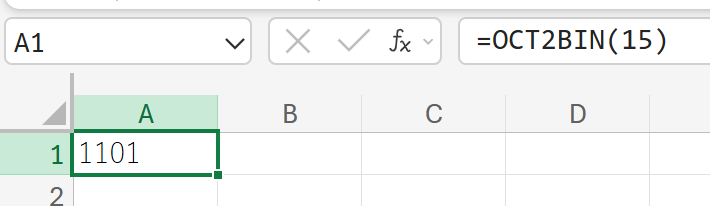
関数の使用例
15(8進数表記)のデータを、2進数に変換しなさい。
OCT2DEC:8進数を10進数に変換
関数の意味
8進数を10進数に変換します。
構文
OCT2DEC(数値)
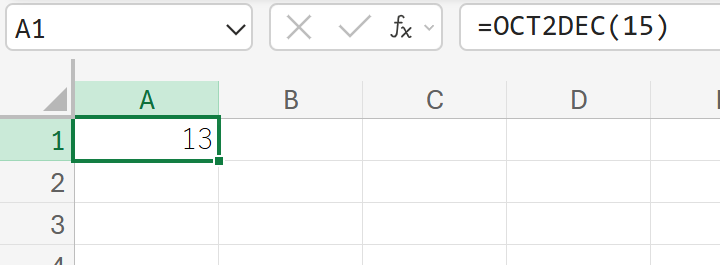
関数の使用例
15(8進数表記)のデータを、10進数に変換しなさい。
OCT2HEX:8進数を16進数に変換
関数の意味
8進数を16進数に変換します。変換後の桁数を指定できます。
構文
OCT2HEX(数値, [桁数])
関数の使用例
15(8進数表記)のデータを、16進数に変換しなさい。
複素数に関する関数(23種類)
複素数は、a+bi の形で表される数で、電気工学(交流回路など)や量子力学などの分野で欠かせません。エクセルの複素数関数は、この複素数の四則演算や高度な数学関数を可能にします。
複素数はエクセル上で「3+4i」や「5-2j」のように文字列として入力する必要があります。
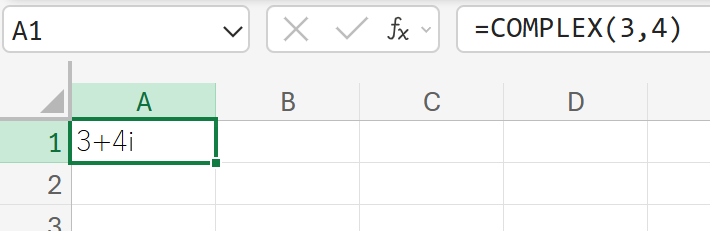
COMPLEX:複素数の作成
実数部と虚数部から複素数を作成します。
関数の意味
指定された実数部と虚数部を用いて、複素数形式の文字列を生成します。
構文
COMPLEX(実数部, 虚数部, [接尾辞])
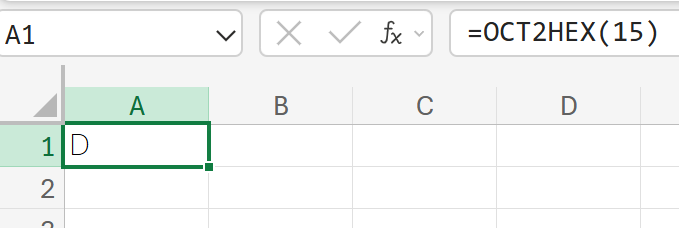
関数の使用例
実数部3、虚数部4の複素数を計算しなさい。
IMABS:複素数の絶対値(モジュラス)
関数の意味
複素数 a+bi の絶対値 a2+b2 を返します。
構文
IMABS(複素数)
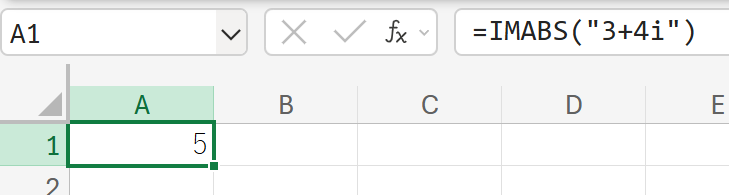
関数の使用例
3+4i(複素数)の絶対値(大きさ)を計算しなさい。
IMAGINARY:複素数の虚数係数
関数の意味
複素数から虚数部分(b)を抽出して返します。
構文
IMAGINARY(複素数)
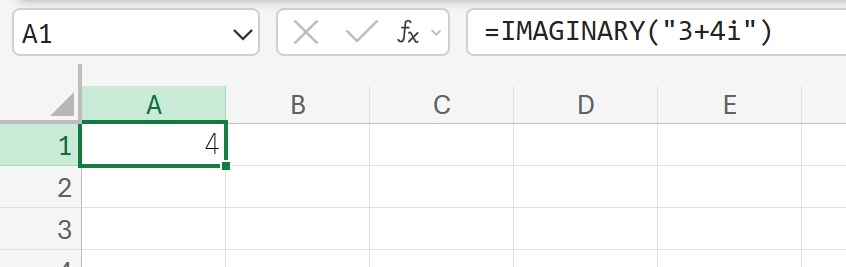
関数の使用例
3+4i(複素数)の虚数部を抽出しなさい。
IMARGUMENT:複素数の偏角
関数の意味
複素数を極形式で表したときの角度(ラジアン単位)を返します。
構文
IMARGUMENT(複素数)
関数の使用例
3+4i(複素数)の偏角をラジアンで計算しなさい。
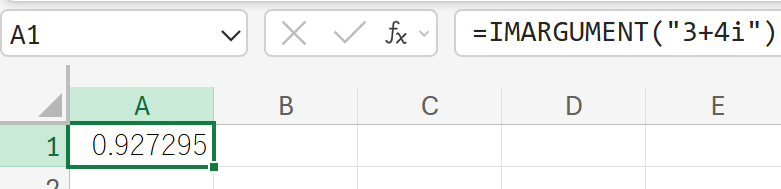
IMCONJUGATE:共役複素数
関数の意味
複素数 a+bi の共役複素数 a−bi を返します。
構文
IMCONJUGATE(複素数)
関数の使用例
3+4i(複素数)の共役複素数を計算しなさい。
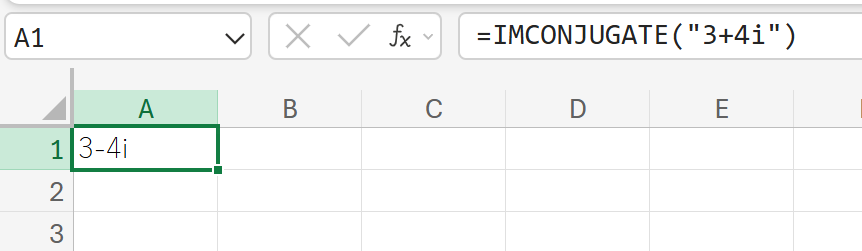
IMCOS:複素数のコサイン
関数の意味
複素数のコサイン (Cosine) を返します。
構文
IMCOS(複素数)
関数の使用例
2i(複素数)の余弦を計算しなさい。
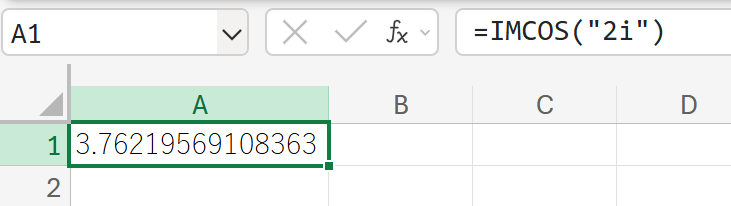
IMCOSH:複素数のハイパーボリックコサイン
関数の意味
複素数のハイパーボリックコサイン (Hyperbolic Cosine) を返します。
構文
IMCOSH(複素数)
関数の使用例
1+i(複素数)の双曲線余弦を計算しなさい。
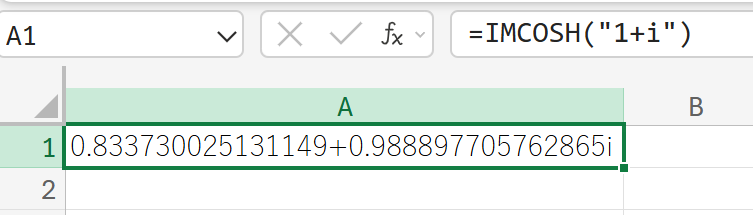
IMCOT:複素数のコタンジェント
関数の意味
複素数のコタンジェント (Cotangent) を返します。
構文
IMCOT(複素数)
関数の使用例
1+i(複素数)の余接を計算しなさい。
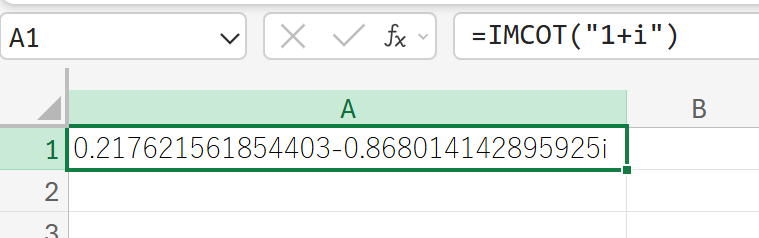
IMCSC:複素数のコセカント
関数の意味
複素数のコセカント (Cosecant) を返します。
構文
IMCSC(複素数)
関数の使用例
1+i(複素数)の余割を計算しなさい。
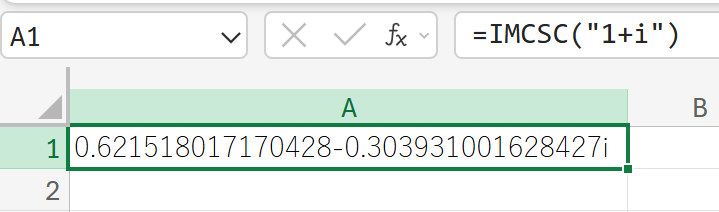
IMCSCH:複素数のハイパーボリックコセカント
関数の意味
複素数のハイパーボリックコセカント (Hyperbolic Cosecant) を返します。
構文
IMCSCH(複素数)
関数の使用例
1+i(複素数)の双曲線余割を計算しなさい。
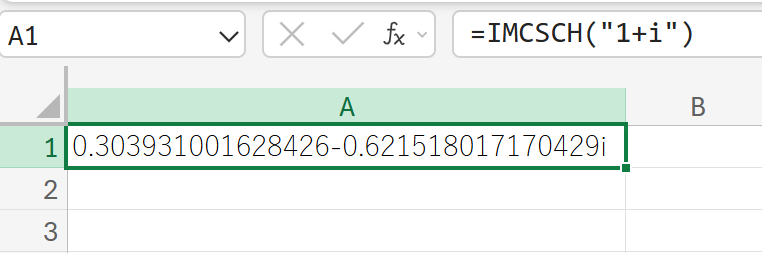
IMDIV:複素数の商(割り算)
関数の意味
2つの複素数の割り算の結果を返します。
構文
IMDIV(複素数1, 複素数2)
関数の使用例
(10+5i)÷(1+2i)の複素数除算を計算しなさい。
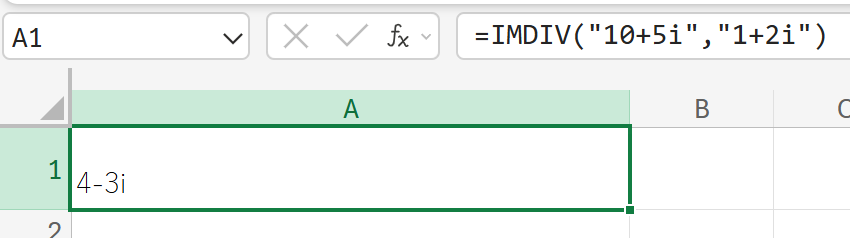
IMEXP:複素数の指数
関数の意味
e を底とする、複素数のべき乗 (e複素数) を返します。
構文
IMEXP(複素数)
関数の使用例
πi(複素数)の指数を計算しなさい。
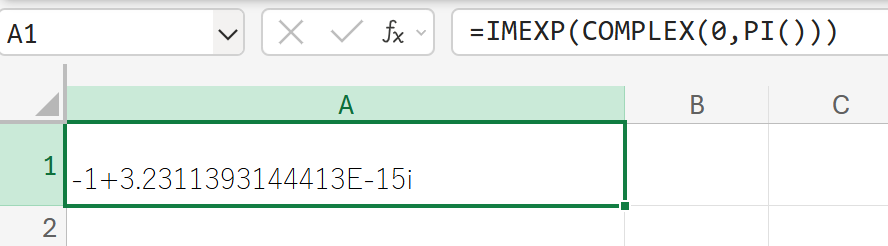
IMLN:複素数の自然対数
関数の意味
複素数の自然対数(底が e の対数)を返します。
構文
IMLN(複素数)
関数の使用例
1+i(複素数)の自然対数を計算しなさい。
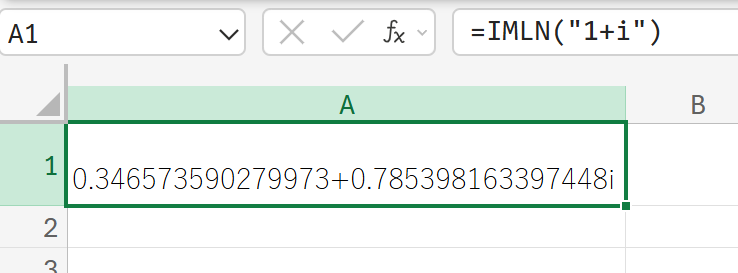
IMLOG10:複素数の10を底とする対数
関数の意味
複素数の10を底とする対数を返します。
構文
IMLOG10(複素数)
関数の使用例
10+10i(複素数)の常用対数を計算しなさい。
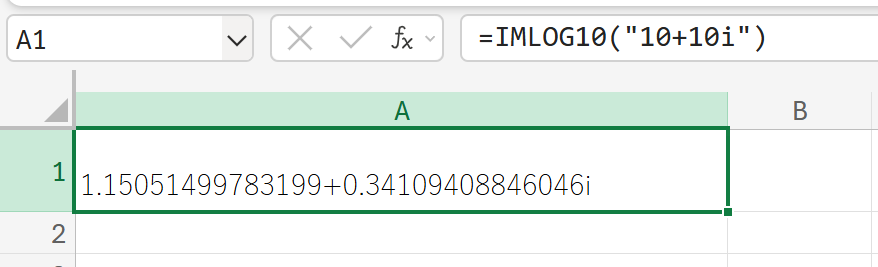
IMLOG2:複素数の2を底とする対数
関数の意味
複素数の2を底とする対数を返します。
構文
IMLOG2(複素数)
関数の使用例
4i(複素数)の二進対数を計算しなさい。
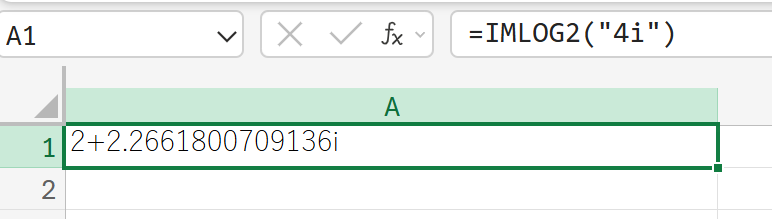
IMPOWER:複素数の累乗
関数の意味
複素数を指定した回数(累乗)だけ掛けた結果を返します。
構文
IMPOWER(複素数, 累乗)
関数の使用例
i3 (虚数単位 i の 3 乗)複素数のべき乗を計算しなさい。
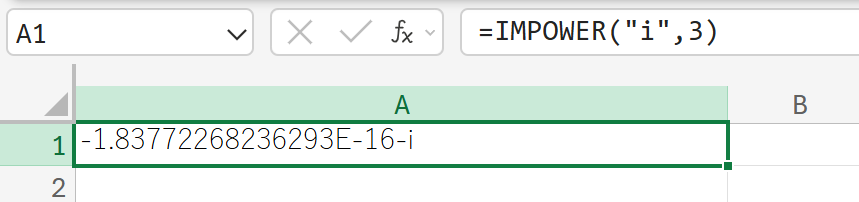
IMPRODUCT:複素数の積(掛け算)
関数の意味
指定された1つまたは複数の複素数を掛け合わせた結果を返します。
構文
IMPRODUCT(複素数1, [複素数2], …)
関数の使用例
複素数 10+2i と 0+1i の積を計算します。
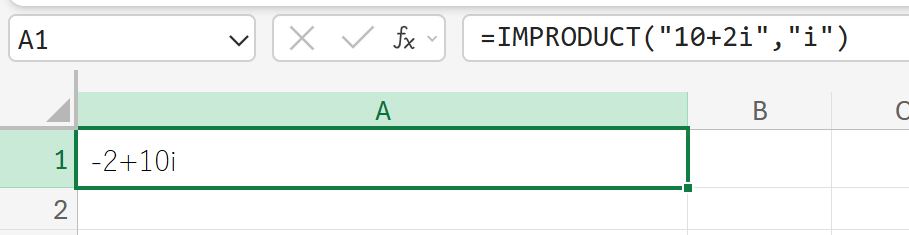
IMREAL:複素数の実数係数
関数の意味
複素数から実数部分(a)を抽出して返します。
構文
IMREAL(複素数)
関数の使用例
−5−12j(複素数)から、実数部を抽出しなさい。
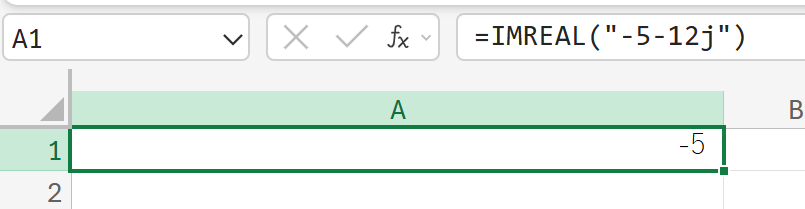
IMSEC:複素数のセカント
関数の意味
複素数のセカント (Secant) を返します。
構文
IMSEC(複素数)
関数の使用例
1+i(複素数)の正割を計算しなさい。
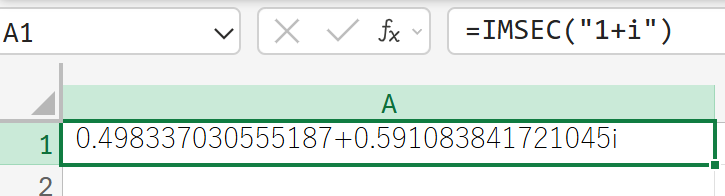
IMSECH:複素数のハイパーボリックセカント
関数の意味
複素数のハイパーボリックセカント (Hyperbolic Secant) を返します。
構文
IMSECH(複素数)
関数の使用例
πj (純虚数)複素数の双曲線正割を計算しなさい。
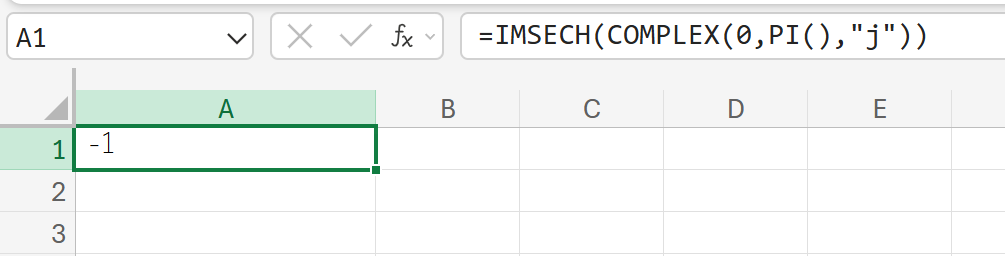
IMSIN:複素数のサイン
関数の意味
複素数のサイン (Sine) を返します。
構文
IMSIN(複素数)
関数の使用例
1+i(複素数)の正弦を計算しなさい。
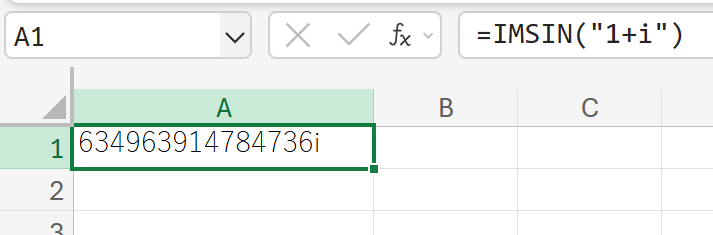
IMSINH:複素数のハイパーボリックサイン
関数の意味
複素数のハイパーボリックサイン (Hyperbolic Sine) を返します。
構文
IMSINH(複素数)
関数の使用例
1+i(複素数)の双曲線正弦を計算しなさい。
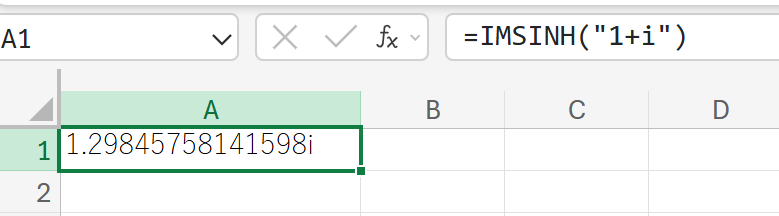
IMSQRT:複素数の平方根
関数の意味
複素数の平方根を返します。
構文
IMSQRT(複素数)
関数の使用例
3+4i(複素数)の平方根を計算しなさい。
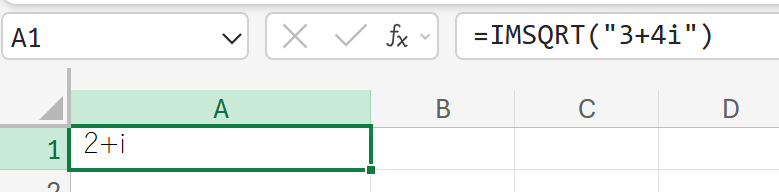
IMSUB:複素数の差(引き算)
関数の意味
2つの複素数の引き算の結果を返します。
構文
IMSUB(複素数1, 複素数2)
関数の使用例
(5+4i)−(1+2i)の複素数減算を計算しなさい。
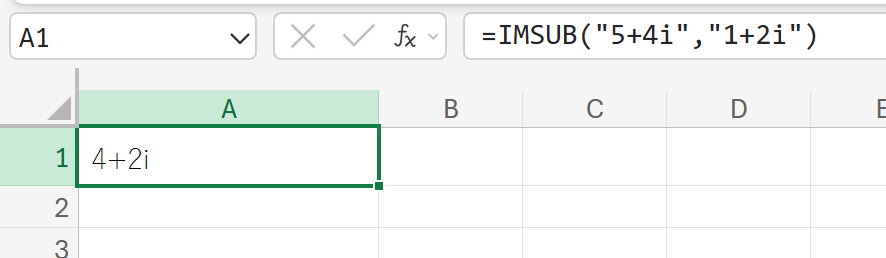
IMSUM:複素数の和(足し算)
関数の意味
指定された1つまたは複数の複素数を足し合わせた結果を返します。
構文
IMSUM(複素数1, [複素数2], …)
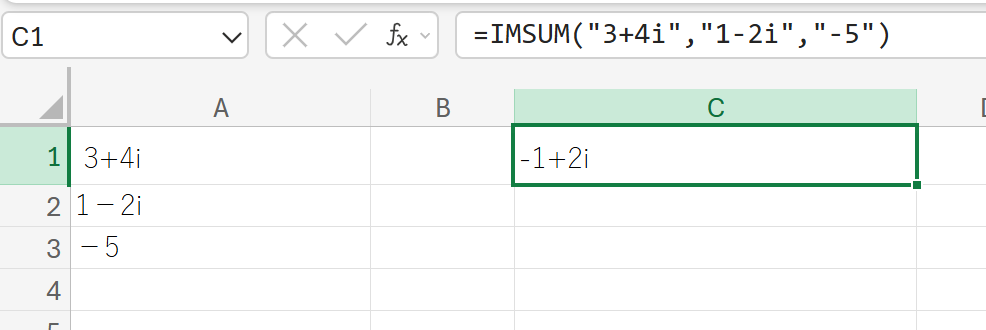
関数の使用例
3つの複素数の合計を計算しなさい。
IMTAN:複素数のタンジェント
関数の意味
複素数のタンジェント (Tangent) を返します。
構文
IMTAN(複素数)
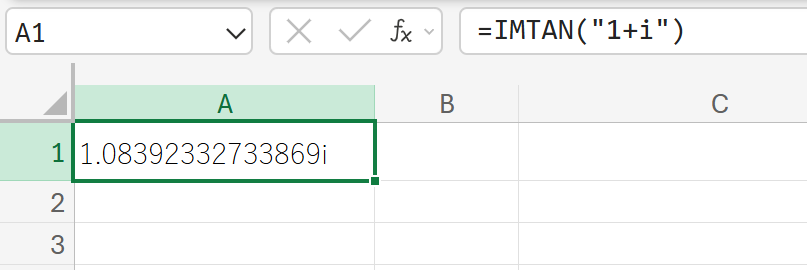
関数の使用例
1+i(複素数)の正接を計算しなさい。
ベッセル関数(4種類)
円筒座標系におけるラプラス方程式やヘルムホルツ方程式の解などとして現れる特殊関数で、物理学や電気通信、信号処理などで使われます。
BESSELI:変形ベッセル関数 I (第1種)
関数の意味
変形ベッセル関数 I (第1種) を返します。
構文
BESSELI(X, 順序)
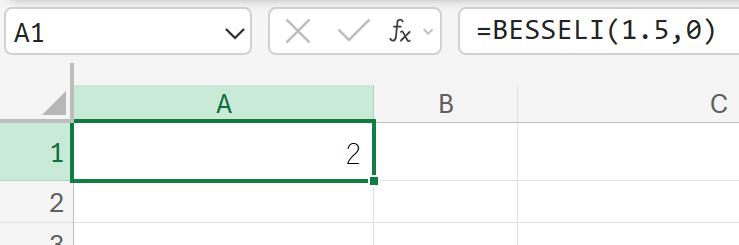
関数の使用例
I0(1.5): X=1.5、順序 ν=0の条件で修正ベッセル関数 Iν(x) の値を計算しなさい。
BESSELJ:ベッセル関数 J (第1種)
関数の意味
ベッセル関数 J (第1種) を返します。
構文
BESSELJ(X, 順序)
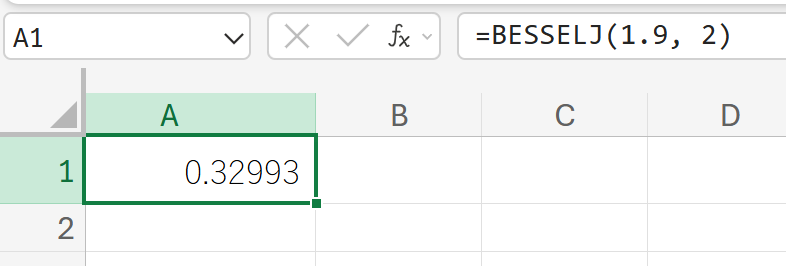
関数の使用例
x=1.9 の 2次の第1種ベッセル関数 J2(1.9) の値を求めます。
BESSELK:変形ベッセル関数 K (第2種)
関数の意味
変形ベッセル関数 K (第2種) を返します。
構文
BESSELK(X, 順序)
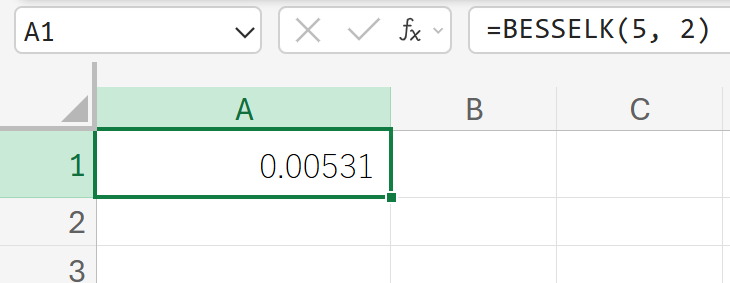
関数の使用例
x=5 の 2次の第2種変形ベッセル関数 K2(5) の値を求めます。
BESSELY:ベッセル関数 Y (第2種)
関数の意味
ベッセル関数 Y (第2種) を返します。
構文
BESSELY(X, 順序)
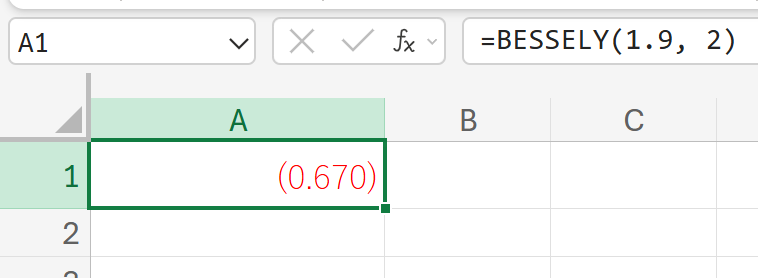
関数の使用例
x=1.9 の 2次の第2種ベッセル関数 Y2(1.9) の値を求めます。
誤差関数(4種類)
正規分布における確率の計算(積分)に関連する関数で、確率論や統計学、物理学で頻繁に使われます。
ERF:誤差関数
関数の意味
誤差関数 erf(x) の値を返します。
構文
ERF(下限, [上限])
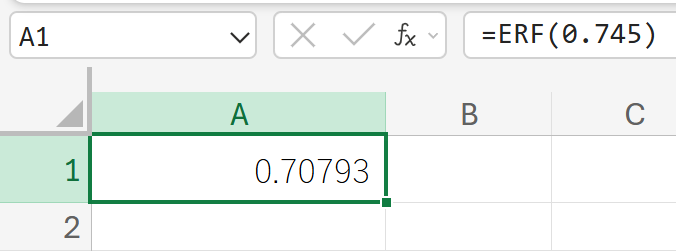
関数の使用例
0 から 0.745 までの積分値を計算します。
ERF.PRECISE:誤差関数(高精度)
関数の意味
誤差関数 erf(x) の値を、より高精度で返します。
構文
ERF.PRECISE(下限, [上限])
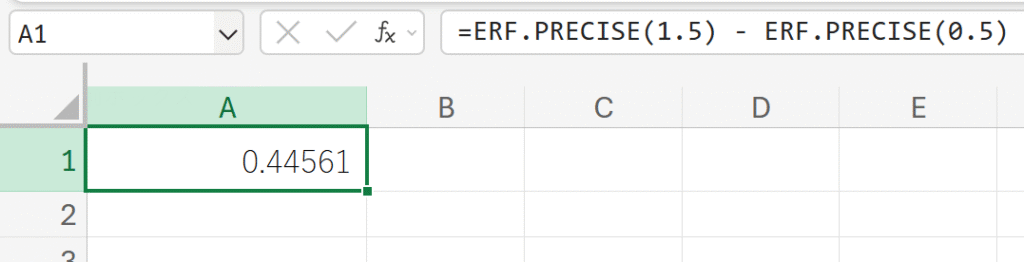
関数の使用例
erf(1.5)−erf(0.5) を計算します。
ERFC:相補誤差関数
関数の意味
相補誤差関数 erfc(x)=1−erf(x) の値を返します。
構文
ERFC(下限)
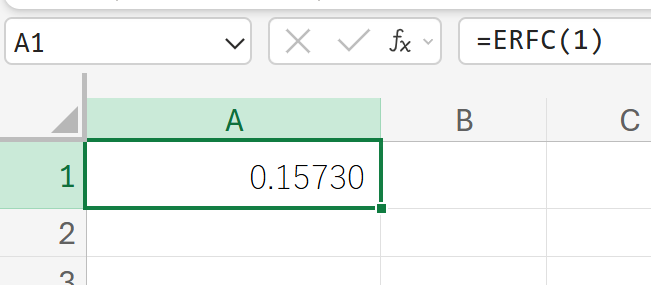
関数の使用例
1から無限大までの積分 erfc(1) を計算します。
ERFC.PRECISE:相補誤差関数(高精度)
関数の意味
相補誤差関数 erfc(x) の値を、より高精度で返します。
構文
ERFC.PRECISE(下限)
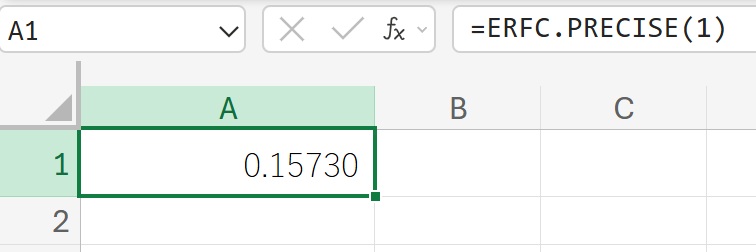
関数の使用例
1から無限大までの積分 erfc(1) を計算します。
その他のエンジニアリング関数(3種類)
進数変換、複素数、ベッセル、誤差関数に分類されない、その他の工学的な計算に役立つ関数です。
CONVERT:単位の変換
異なる単位間で数値を変換します。最も利用頻度が高いエンジニアリング関数の一つです。
関数の意味
メートル、ポンド、馬力、摂氏など、さまざまな測定単位間で値を変換します。
構文
CONVERT(数値, 換算前単位, 換算後単位)
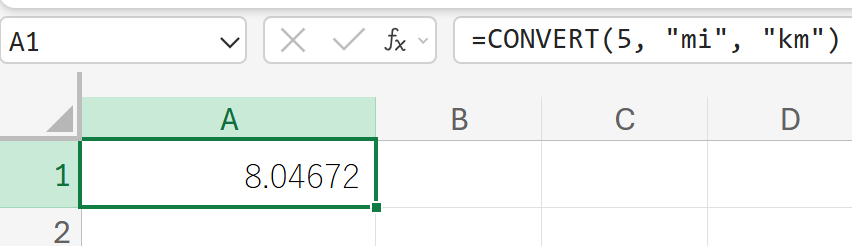
関数の使用例
5マイルをキロメートルに変換します。
DELTA:クロネッカーのデルタ
関数の意味
2つの数値が等しいかどうかを判定するクロネッカーのデルタを返します。等しい場合は 1、等しくない場合は 0 を返します。
構文
DELTA(数値1, [数値2])
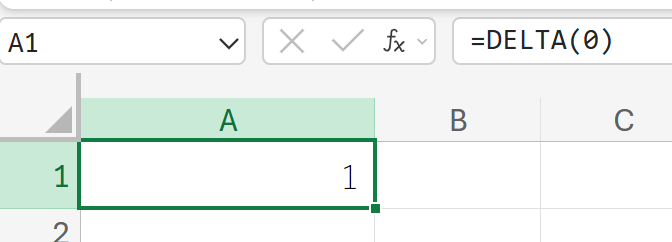
関数の使用例
0と0が等しいか確認します。
GESTEP:ヘヴィサイドの階段関数
関数の意味
数値がステップ値以上であるかどうかを判定するヘヴィサイドの階段関数を返します。数値 ≥ ステップ値の場合は 1、そうでない場合は 0 を返します。
構文
GESTEP(数値, [ステップ])
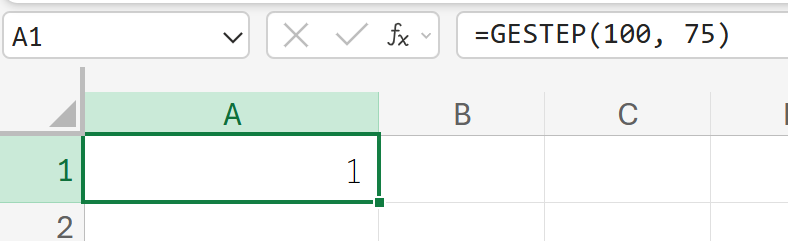
関数の使用例
100は75以上なので 1 を返します。
まとめ:エンジニアリング関数を使いこなそう!
エクセルOffice 365で使えるエンジニアリング関数全54種類を一つひとつ見てきました。
| 関数の種類 | 主な役割 | 特徴的な関数名 |
| 進数変換 | 10進数、2進数、16進数、8進数の相互変換 | DEC2BIN, HEX2DEC, OCT2HEX |
| 複素数 | 複素数の四則演算や三角関数、対数などの計算 | COMPLEX, IMSUM, IMEXP, IMABS |
| ビット演算 | ビット単位での論理演算やシフト演算 | BITAND, BITLSHIFT, BITXOR |
| 特殊関数 | 工学や物理学で使われる高度な数学関数 | BESSELJ, ERF |
| その他 | 単位変換や比較判定 | CONVERT, DELTA, GESTEP |
普段の業務で「こんな計算、エクセルでできるのかな?」と感じた時は、ぜひこの記事に戻ってエンジニアリング関数をチェックしてみてください。
特に進数変換やCONVERT関数は、IT分野や測定値を扱う場面で非常に役立ちます。また、複素数計算を必要とする上級者の方には、IM*系の関数が強力な助けとなるはずです。
全54種類の関数をすべて覚える必要はありません。必要な時に「こういう関数があるんだ!」と思い出せるよう、この記事をブックマークしておいてくださいね。
📚 Excelをもっと学びたい方へ
Excelスキルが向上すると、
など、日々の仕事が格段に楽になります。
しかし、Excelスキルは目に見えにくいため、転職や昇進の場面で正しく評価されないことも少なくありません。
そこでおすすめなのが、Excelスキルを客観的に証明できるMOS資格です。
MOS資格を本気で取得したい方へ
Excelを実務レベルで使いこなしたいなら、MOS資格の取得がおすすめです。MOSはExcelスキルを客観的に証明できるため、転職や昇進でも高く評価されます。
ハロー!パソコン教室のMOS対策講座は、初心者でも合格を目指せるオンライン講座です。
ハロー!パソコン教室 MOS対策講座の特徴
こんな方におすすめ

独学に不安がある方は、公式サイトで講座内容を確認してみてください。
\ Excelスキルを証明するならMOS資格 /





コメント