エクセルoffice365で使える統計関数104種類徹底解説！

「エクセルの統計関数って全部で何個あるんだろう？」

「どの関数を使えばデータが分析できるの？」

こんな疑問が湧いたのでOffice365で使える統計関数を実際に調べてみました。

Microsoft 365（Office 365）で使える統計関数は、全部で104種類あります！

この記事では、統計関数全104種類を解説していきます。

この記事で分かること

Excel統計関数の網羅的な知識
実務的なデータ分析手法
類似関数の使い分け

そもそもExcelの「統計関数」とは？
【全104種類】Excelで使える統計関数一覧表
統計関数の種類と使い方【分類別解説】
記事のまとめと結びの言葉
1. Excel統計関数 104 種類の総まとめ

そもそもExcelの「統計関数」とは？

統計関数とは

統計的な計算を行うためにエクセルに組み込まれた関数

たとえば、クラスのテストの点数の平均を出したいとき、点数を一つひとつ合計して人数で割る作業は面倒ですよね。統計関数を使えば、AVERAGE関数のように、範囲を指定するだけで一瞬で平均値が計算できます。

統計関数が担う役割は、単なる平均の計算だけではありません。

統計関数でできること

データを要約する：
平均、最小値、最大値、中央値などを求める
データの散らばりを知る：
分散、標準偏差などを求める
データの関係性を探る：
相関係数や回帰分析を行う
確率を計算する：
正規分布や二項分布などの確率を求める
仮説を検証する：
t検定やF検定などの統計的な検定を行う

これらの関数を使いこなせると、データから見えない真実を読み解くことができるようになります。

でんちゃん

「この商品の売上が伸びたのは本当にキャンペーンのおかげか？」といった疑問を、客観的な数値で判断できるようになるのです。

【全104種類】Excelで使える統計関数一覧表

ここからは、Microsoft 365で利用可能な統計関数全104種類を一覧でご紹介します。

【統計関数一覧表】

統計関数の種類	関数名	構文 (引数)	関数の意味
カウント/集計	COUNT	COUNT(値1, [値2], …)	数値が含まれるセルの個数を数える
	COUNTA	COUNTA(値1, [値2], …)	空白ではないセルの個数を数える
	COUNTBLANK	COUNTBLANK(範囲)	指定された範囲に含まれる空白セルの個数を数える
	COUNTIF	COUNTIF(範囲, 検索条件)	指定された条件を満たすセルの個数を数える
	COUNTIFS	COUNTIFS(範囲1, 条件1, [範囲2, 条件2], …)	複数の条件を満たすセルの個数を数える
平均/中央値/最頻値	AVERAGE	AVERAGE(数値1, [数値2], …)	引数の平均 (算術平均) を返す
	AVERAGEA	AVERAGEA(値1, [値2], …)	数値、文字列、論理値を含む引数の平均を返す
	AVERAGEIF	AVERAGEIF(範囲, 検索条件, [平均対象範囲])	指定された条件を満たすすべてのセルの平均を計算する
	AVERAGEIFS	AVERAGEIFS(平均対象範囲, 範囲1, 条件1, …)	複数の条件を満たすすべてのセルの平均を計算する
	MEDIAN	MEDIAN(数値1, [数値2], …)	与えられた数値の中央値を返す
	MODE.MULT	MODE.MULT(数値1, [数値2], …)	配列またはセル範囲内のデータの最頻値 (最も頻繁に出現する値) を垂直配列として返す
	MODE.SNGL	MODE.SNGL(数値1, [数値2], …)	配列またはセル範囲内のデータの最頻値を返す
	GEOMEAN	GEOMEAN(数値1, [数値2], …)	相対成長率を計算する際の幾何平均を返す
	HARMEAN	HARMEAN(数値1, [数値2], …)	母集団の調和平均を返す
	TRIMMEAN	TRIMMEAN(配列, 割合)	データセットの両端からデータ要素の一定の割合を除外した平均を返す
最小値/最大値	MAX	MAX(数値1, [数値2], …)	引数リストの最大値を返す
	MAXA	MAXA(値1, [値2], …)	論理値や文字列を含む引数リストの最大値を返す
	MAXIFS	MAXIFS(最大範囲, 範囲1, 条件1, …)	複数の条件を満たすセルの中から最大値を返す
	MIN	MIN(数値1, [数値2], …)	引数リストの最小値を返す
	MINA	MINA(値1, [値2], …)	論理値や文字列を含む引数リストの最小値を返す
	MINIFS	MINIFS(最小範囲, 範囲1, 条件1, …)	複数の条件を満たすセルの中から最小値を返す
順位/パーセンタイル	LARGE	LARGE(配列, K)	データセット内の K 番目に大きな値を返す
	SMALL	SMALL(配列, K)	データセット内の K 番目に小さな値を返す
	RANK.AVG	RANK.AVG(数値, 参照, [順序])	数値リストの中での順位を返す (重複する値には平均順位を返す)
	RANK.EQ	RANK.EQ(数値, 参照, [順序])	数値リストの中での順位を返す (重複する値には同じ順位を返す)
	PERCENTILE.EXC	PERCENTILE.EXC(配列, K)	0 と 1 を除く範囲の K 番目のパーセンタイル値を返す
	PERCENTILE.INC	PERCENTILE.INC(配列, K)	0 と 1 を含む範囲の K 番目のパーセンタイル値を返す
	QUARTILE.EXC	QUARTILE.EXC(配列, 四分位)	0 と 4 を除く範囲のデータセットの四分位数を返す
	QUARTILE.INC	QUARTILE.INC(配列, 四分位)	0 と 4 を含む範囲のデータセットの四分位数を返す
分散/標準偏差	AVEDEV	AVEDEV(数値1, [数値2], …)	データの平均からの絶対偏差の平均を返す
	DEVSQ	DEVSQ(数値1, [数値2], …)	標本の平均からの偏差の平方和を返す
	VAR.P	VAR.P(数値1, [数値2], …)	母集団全体に基づいて分散を計算する (論理値や文字列は無視)
	VAR.S	VAR.S(数値1, [数値2], …)	標本に基づいて分散を計算する (論理値や文字列は無視)
	VARA	VARA(値1, [値2], …)	母集団に基づいて分散を計算する (論理値や文字列を含む)
	VARPA	VARPA(値1, [値2], …)	母集団全体に基づいて分散を計算する (論理値や文字列を含む)
	STDEV.P	STDEV.P(数値1, [数値2], …)	母集団全体に基づいて標準偏差を計算する (論理値や文字列は無視)
	STDEV.S	STDEV.S(数値1, [数値2], …)	標本に基づいて標準偏差を計算する (論理値や文字列は無視)
	STDEVA	STDEVA(値1, [値2], …)	標本に基づいて標準偏差を計算する (論理値や文字列を含む)
	STDEVPA	STDEVPA(値1, [値2], …)	母集団全体に基づいて標準偏差を計算する (論理値や文字列を含む)
回帰分析/相関	CORREL	CORREL(配列1, 配列2)	2 つのデータセット間の相関係数を返す
	COVARIANCE.P	COVARIANCE.P(配列1, 配列2)	2 つのデータセット間の母集団共分散を返す
	COVARIANCE.S	COVARIANCE.S(配列1, 配列2)	2 つのデータセット間の標本共分散を返す
	RSQ	RSQ(既知の y, 既知の x)	ピアソンの積率相関係数の 2 乗を返す
	PEARSON	PEARSON(配列1, 配列2)	ピアソンの積率相関係数を返す
	INTERCEPT	INTERCEPT(既知の y, 既知の x)	線形回帰直線の切片を計算する
	SLOPE	SLOPE(既知の y, 既知の x)	線形回帰直線の傾きを計算する
	STEYX	STEYX(既知の y, 既知の x)	回帰における標準誤差を返す
	FORECAST.LINEAR	FORECAST.LINEAR(X, 既知の y, 既知の x)	既存の値に基づいて将来の値を予測する
	GROWTH	GROWTH(既知の y, [既知の x], [新しい x], [定数])	指数曲線に沿って成長率を予測する
	LINEST	LINEST(既知の y, [既知の x], [定数], [統計])	既知のデータを使用して、データの最小二乗法による直線回帰を計算する
	LOGEST	LOGEST(既知の y, [既知の x], [定数], [統計])	既知のデータを使用して、指数回帰曲線を計算する
	TREND	TREND(既知の y, [既知の x], [新しい x], [定数])	線形の傾向を返す
記述統計量	KURT	KURT(数値1, [数値2], …)	データセットの尖度を返す
	SKEW	SKEW(数値1, [数値2], …)	分布の歪度を返す
	SKEW.P	SKEW.P(数値1, [数値2], …)	母集団に基づく分布の歪度を返す
	FREQUENCY	FREQUENCY(データ配列, 区間配列)	値の頻度分布を垂直配列で計算する
確率/分布 (一般)	BETA.DIST	BETA.DIST(x, α, β, 累積, [A], [B])	ベータ分布の累積分布関数の値または確率密度関数の値を返す
	BETA.INV	BETA.INV(確率, α, β, [A], [B])	ベータ分布の累積分布関数の逆関数値を返す
	GAMMA.DIST	GAMMA.DIST(x, α, β, 累積)	ガンマ分布の値を返す
	GAMMA.INV	GAMMA.INV(確率, α, β)	ガンマ分布の累積分布関数の逆関数値を返す
	GAMMALN	GAMMALN(x)	ガンマ関数の自然対数を返す
	GAMMALN.PRECISE	GAMMALN.PRECISE(x)	ガンマ関数の自然対数を返す
	GAMMA	GAMMA(x)	ガンマ関数値を返す
	LOGNORM.DIST	LOGNORM.DIST(x, 平均, 標準偏差, 累積)	対数正規分布の累積分布関数または確率密度関数の値を返す
	LOGNORM.INV	LOGNORM.INV(確率, 平均, 標準偏差)	対数正規分布の累積分布関数の逆関数値を返す
	WEIBULL.DIST	WEIBULL.DIST(x, α, β, 累積)	ワイブル分布の値を返す
確率/分布 (離散)	BINOM.DIST	BINOM.DIST(成功数, 試行回数, 成功率, 累積)	二項分布の確率を返す
	BINOM.DIST.RANGE	BINOM.DIST.RANGE(試行回数, 成功率, S, [S2])	二項分布の確率を計算する (範囲指定可能)
	BINOM.INV	BINOM.INV(試行回数, 成功率, α)	基準以下の二項分布の累積確率の最大値を返す
	HYPGEOM.DIST	HYPGEOM.DIST(成功数, 標本数, 母集団の成功数, 母集団の大きさ, 累積)	超幾何分布の確率を返す
	NEGBINOM.DIST	NEGBINOM.DIST(失敗数, 成功数, 成功率, 累積)	負の二項分布の確率を返す
	POISSON.DIST	POISSON.DIST(x, 平均, 累積)	ポアソン分布の確率を返す
確率/分布 (正規)	NORM.DIST	NORM.DIST(x, 平均, 標準偏差, 累積)	正規分布の累積分布関数または確率密度関数の値を返す
	NORM.INV	NORM.INV(確率, 平均, 標準偏差)	正規分布の累積分布関数の逆関数値を返す
	NORM.S.DIST	NORM.S.DIST(Z, 累積)	標準正規分布の累積分布関数の値を返す
	NORM.S.INV	NORM.S.INV(確率)	標準正規分布の累積分布関数の逆関数値を返す
	GAUSS	GAUSS(Z)	標準正規分布の累積分布関数の値から 0.5 を引いた値を返す
	STANDARDIZE	STANDARDIZE(x, 平均, 標準偏差)	正規化された値を返す
確率/分布 (その他)	PHI	PHI(X)	標準正規分布の確率密度関数の値を返す
	PROB	PROB(x 範囲, 確率範囲, 下限, [上限])	指定された範囲の値が特定の値の間にある確率を返す
検定/区間推定	CONFIDENCE.NORM	CONFIDENCE.NORM(α, 標準偏差, 標本サイズ)	正規分布の母平均に対する信頼区間の半値を返す
	CONFIDENCE.T	CONFIDENCE.T(α, 標準偏差, 標本サイズ)	スチューデントの t 分布を使用して母集団の平均の信頼区間の半値を返す
	CHISQ.TEST	CHISQ.TEST(実測値の範囲, 期待値の範囲)	独立性のカイ二乗検定の結果を返す
	F.TEST	F.TEST(配列1, 配列2)	F 検定の結果を返す
	T.TEST	T.TEST(配列1, 配列2, 尾部, タイプ)	t 検定に関連付けられた確率を返す
	Z.TEST	Z.TEST(配列, x, [σ])	Z 検定の片側 P 値を返す
	CHISQ.DIST	CHISQ.DIST(x, 自由度, 累積)	カイ二乗分布の値を返す
	CHISQ.DIST.RT	CHISQ.DIST.RT(x, 自由度)	カイ二乗分布の右側確率を返す
	CHISQ.INV	CHISQ.INV(確率, 自由度)	カイ二乗分布の累積分布関数の逆関数値を返す
	CHISQ.INV.RT	CHISQ.INV.RT(確率, 自由度)	カイ二乗分布の右側確率の逆関数値を返す
	F.DIST	F.DIST(x, 自由度1, 自由度2, 累積)	F 分布の値を返す
	F.DIST.RT	F.DIST.RT(x, 自由度1, 自由度2)	F 分布の右側確率を返す
	F.INV	F.INV(確率, 自由度1, 自由度2)	F 分布の累積分布関数の逆関数値を返す
	F.INV.RT	F.INV.RT(確率, 自由度1, 自由度2)	F 分布の右側確率の逆関数値を返す
	T.DIST	T.DIST(x, 自由度, 尾部)	スチューデントの t 分布の値を返す
	T.DIST.2T	T.DIST.2T(x, 自由度)	スチューデントの t 分布の両側確率を返す
	T.DIST.RT	T.DIST.RT(x, 自由度)	スチューデントの t 分布の右側確率を返す
	T.INV	T.INV(確率, 自由度)	スチューデントの t 分布の累積分布関数の逆関数値を返す
	T.INV.2T	T.INV.2T(確率, 自由度)	スチューデントの t 分布の両側確率の逆関数値を返す
その他	FISHER	FISHER(r)	フィッシャー変換を返す
	FISHERINV	FISHERINV(y)	フィッシャー逆変換を返す
	PERMUT	PERMUT(総数, 選択数)	特定の個数を選択するときの順列の数を返す (順序を考慮)
	PERMUTATIONA	PERMUTATIONA(総数, 選択数)	特定の個数を選択するときの順列の数を返す (重複を考慮)

統計関数の種類と使い方【分類別解説】

ここからは、上でご紹介した104種類の関数を一つひとつ、関数の意味、構文、具体的な使用例を通して解説していきます。

1. COUNT 関数

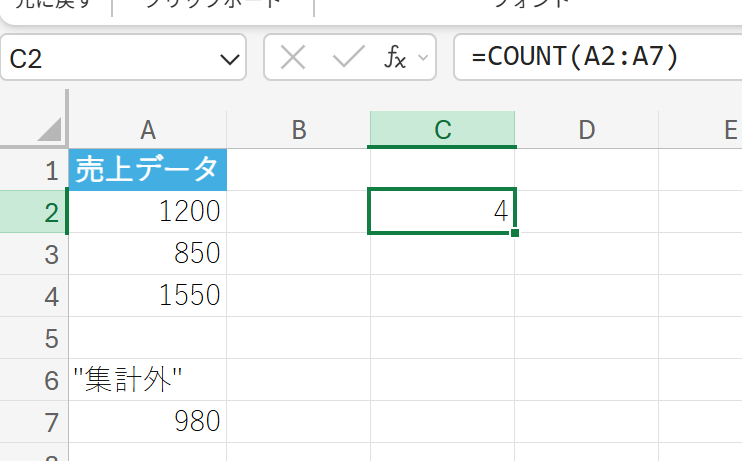
COUNT 関数は、セル範囲に含まれる数値の個数を数えます。

数字だけを数えたい場合に非常に便利です。文字列や空白のセルは無視されます。

関数の構文

COUNT(値1, [値2], …)

値1, [値2], …：個数を数えたいセル範囲または値を指定します。

関数の使用例

商品の売上データのうち、実際に数値（金額）が入力されているセルの数を数えて、データが揃っているか確認します。

2. COUNTA 関数

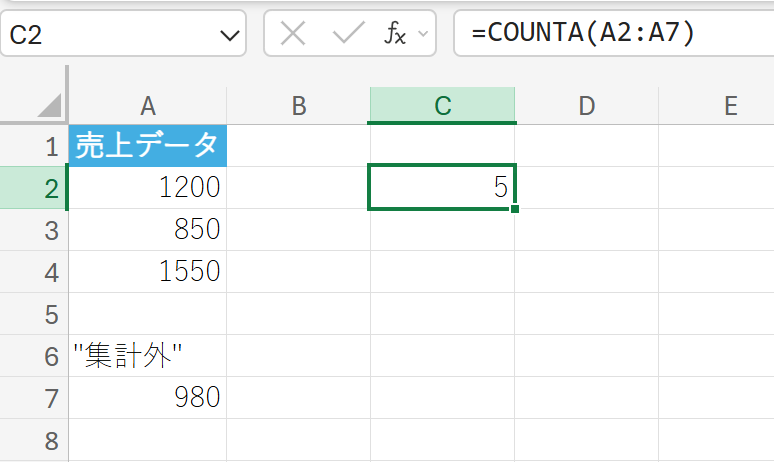
COUNTA 関数は、セル範囲に含まれる空白ではないセルの個数を数えます。

つまり、数値、文字列、論理値、エラー値など、何かしらのデータが入力されていればすべてカウントの対象となります。データが入力されている総数を把握したい場合に役立ちます。

関数の構文

COUNTA(値1, [値2], …)

値1, [値2], …：個数を数えたいセル範囲または値を指定します。

関数の使用例

上記と同じ売上データを使用し、空白のセルを除いた、データが入力されている項目の総数を数えます。

3. COUNTBLANK 関数

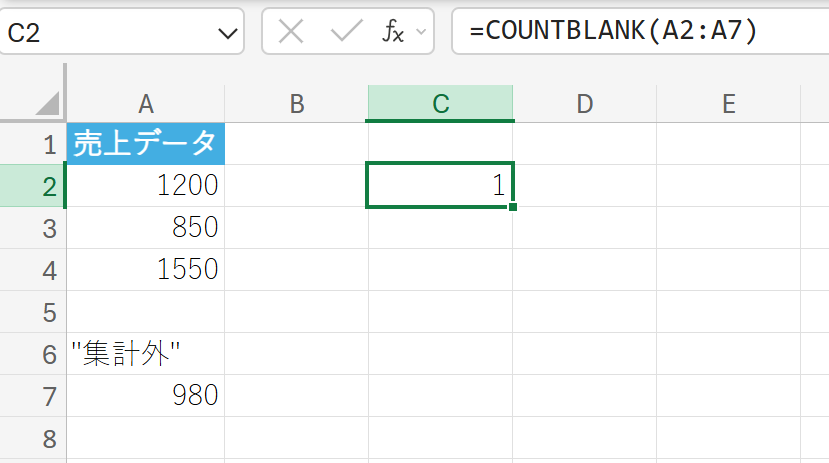
COUNTBLANK 関数は、指定された範囲に含まれる空白セルの個数を数えます。

データ入力が漏れている箇所を簡単にチェックしたいときに便利です。

関数の構文

COUNTBLANK(範囲)

範囲：空白セルの個数を数えたいセル範囲を指定します。

関数の使用例

上記と同じ売上データを使用し、データが未入力（空白）のセルの数を数えます。

4. COUNTIF 関数

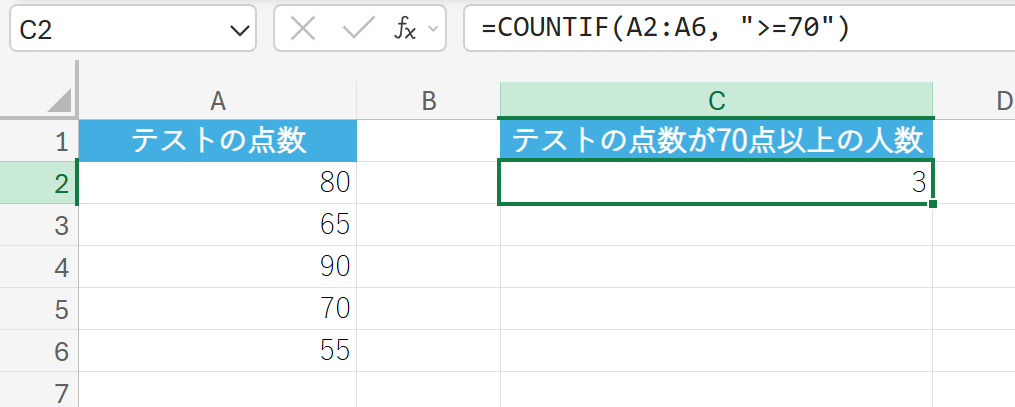
COUNTIF 関数は、指定された条件を満たすセルの個数を数えます。

単一の条件に基づいてデータをカウントしたい場合に便利な関数です。「80点以上の人が何人いるか」「特定の部署の社員が何人いるか」といった集計に使います。

関数の構文

COUNTIF(範囲, 検索条件)

範囲：条件を適用するセル範囲を指定します。
検索条件：個数を数える対象とする条件を、数値、文字列、または式で指定します。

関数の使用例

テストの点数データを使用して、70点以上の生徒が何人いるか集計します。

5. COUNTIFS 関数

COUNTIFS 関数は、複数の条件を満たすセルの個数を数えます。

COUNTIFと異なり、最大127個の条件を指定できるため、「営業部の女性社員で、かつ売上が100万円以上」といった、より複雑な絞り込み集計が可能になります。

関数の構文

COUNTIFS(範囲1, 条件1, [範囲2, 条件2], …)

範囲1, 範囲2, …：それぞれの条件を適用するセル範囲を指定します。
条件1, 条件2, …：それぞれの範囲に対応する条件を指定します。

関数の使用例

社員の部署と性別データを使用して、「営業部」かつ「女性」の社員数を集計します。

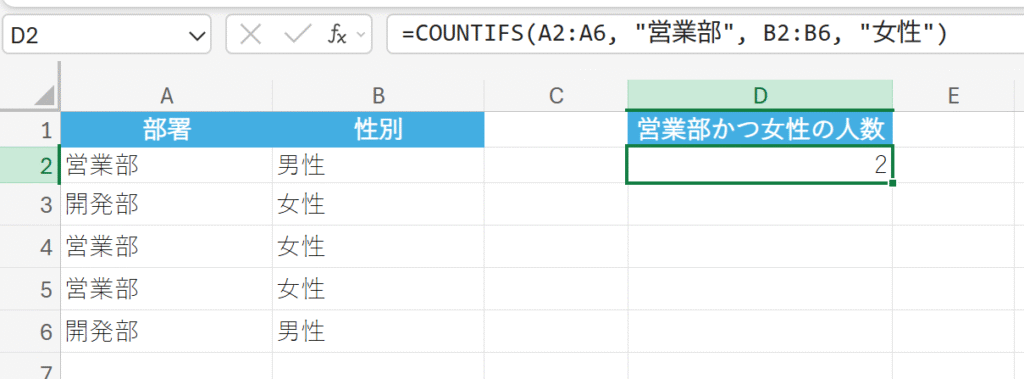
6. AVERAGE 関数

AVERAGE 関数は、引数リストに含まれる数値の平均 (算術平均) を返します。

最も一般的で、利用頻度の高い平均の計算方法です。すべての値を合計し、その数値の個数で割った値を求めます。

関数の構文

AVERAGE(数値1, [数値2], …)

数値1, [数値2], …：平均を求めたい、数値、または数値を含む配列やセル範囲を指定します。

関数の使用例

あるクラスのテストの点数データを使用して、クラスの平均点を計算します。

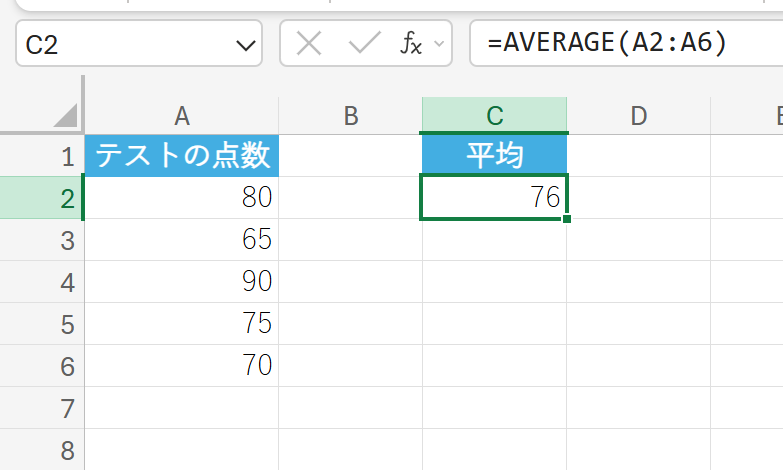
7. AVERAGEA 関数

AVERAGEA 関数は、数値、文字列、論理値を含む引数の平均を返します。

AVERAGE関数との大きな違いは、引数の中に含まれ文字列を「0」として、論理値の TRUEを「1」、FALSEを「0」として計算の対象に含める点です。特に、データの中に文字列や論理値が混ざっている場合に使用します。

関数の構文

AVERAGEA(値1, [値2], …)

値1, [値2], …：平均を求めたい、数値、文字列、論理値などを含む配列やセル範囲を指定します。

関数の使用例

テストの点数データに、欠席者を表す「欠席」という文字列と、ボーナスポイントを表す TRUE を含めて平均を計算します。

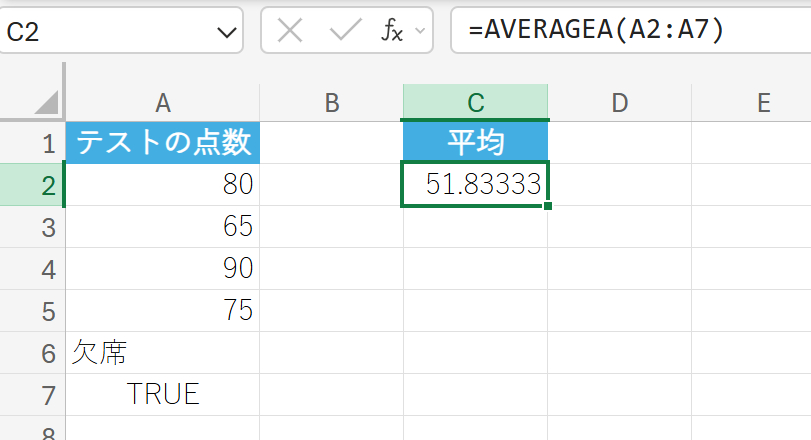
解説

合計(80+65+90+75+0+1 = 311)を6個（文字列「欠席」は0としてカウント）で割った 311/6 の結果です。

8. AVERAGEIF 関数

AVERAGEIF 関数は、指定された条件を満たすすべてのセルの平均を計算します。

「特定の部署の社員の平均売上」「80点以上の生徒の平均点」など、単一の条件でデータを絞り込んで平均を求めたい場合に便利です。

関数の構文

AVERAGEIF(範囲, 検索条件, [平均対象範囲])

範囲：条件を適用するセル範囲を指定します。
検索条件：平均対象とする条件を、数値、文字列、または式で指定します。
平均対象範囲：実際に平均を求める数値を含むセル範囲です。省略すると、「範囲」自体が平均対象範囲になります。

関数の使用例

商品の種類と売上金額のデータを使用して、「A商品」の売上のみの平均を求めます。

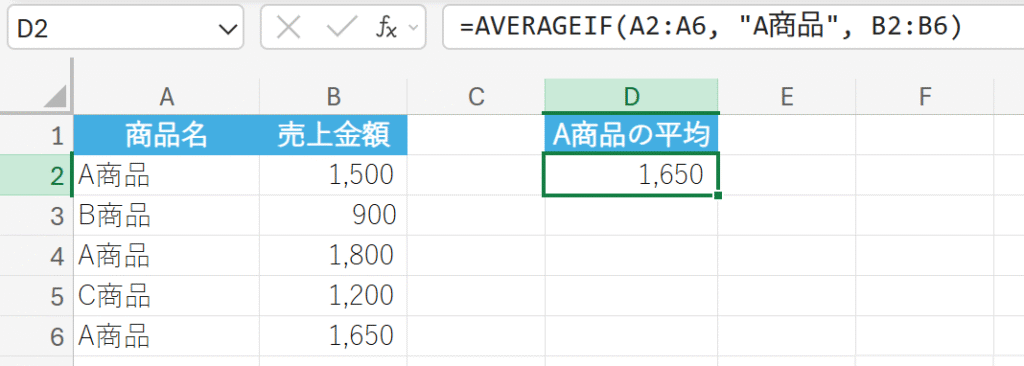
9. AVERAGEIFS 関数

AVERAGEIFS 関数は、複数の条件を満たすすべてのセルの平均を計算します。

AVERAGEIFが単一条件なのに対し、AVERAGEIFSは複数の条件（最大127個）を同時に指定できます。「営業部の女性社員」や「関東エリアで売上目標を達成した店舗」など、より高度な絞り込み平均を求めたいときに使います。

関数の構文

AVERAGEIFS(平均対象範囲, 範囲1, 条件1, [範囲2, 条件2], …)

平均対象範囲：実際に平均を求める数値を含むセル範囲です。この引数は省略できません。
範囲1, 条件1, …：それぞれの条件を適用するセル範囲と条件を指定します。

関数の使用例

商品の種類、エリア、売上金額のデータを使用して、「A商品」かつ「関東エリア」の売上のみの平均を求めます。

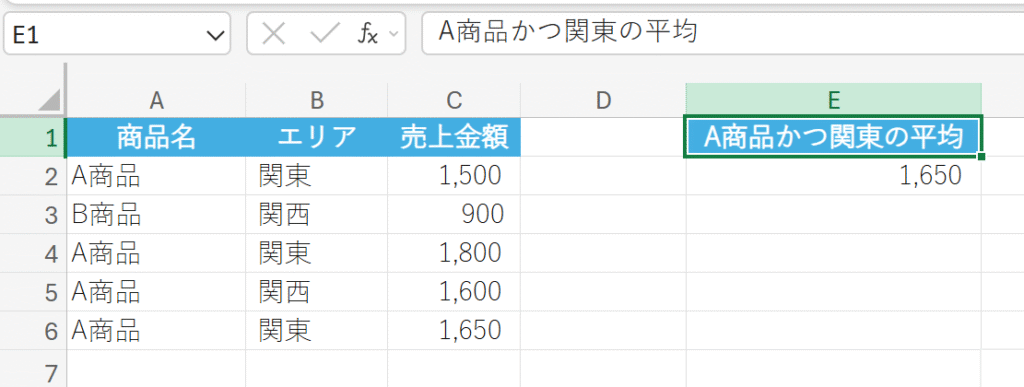
解説

1,500円、1,800円、1,650円の平均です。 (1500+1800+1650)/3 = 1650

10. AVEDEV 関数

AVEDEV 関数は、データポイントの平均値からの絶対偏差の平均を返します。

簡単に言うと、データが平均値からどれくらい散らばっているかを示す指標の一つです。値が大きいほど、データは平均から大きく離れて散らばっていることになり、逆に値が小さいほどデータは平均値の周りに集中していることを示します。

関数の構文

AVEDEV(数値1, [数値2], …)

数値1, [数値2], …：平均からの絶対偏差の平均を求めたい、数値を含むセル範囲を指定します。

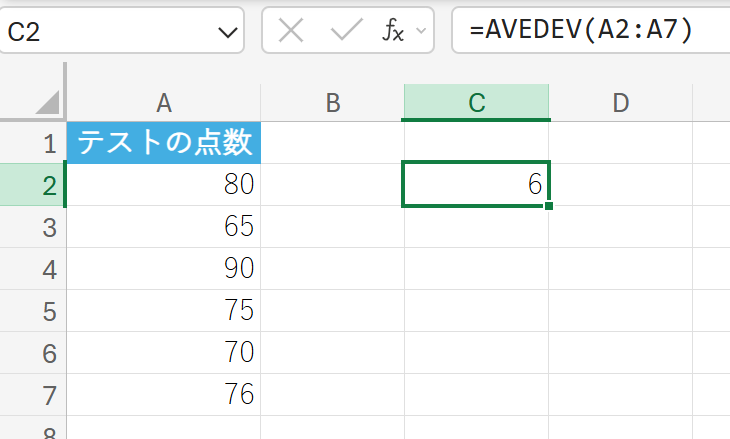
関数の使用例

あるクラスのテストの点数データを使用して、平均からの散らばり具合を計算します。

11. BETA.DIST 関数

BETA.DIST 関数は、ベータ分布の累積分布関数の値または確率密度関数の値を返します。

ベータ分布は、主にプロジェクト計画や財務分析で、確率的な発生時間をモデル化するのに使用される関数です。

関数の構文

BETA.DIST(x, α, β, 累積, [A], [B])

x：分布を評価する値を指定します。
α：分布のパラメーターを指定します。
β：分布のパラメーターを指定します。
累積：論理値で、TRUE（累積分布関数）またはFALSE（確率密度関数）を指定します。
[A], [B]：分布の下限と上限を指定します。省略可能です。

関数の使用例

ベータ分布を使って、あるプロジェクトが特定の期間内に完了する確率を求めます。このプロジェクトが 2 日以内に完了する確率はいくつでしょうか？

12. BETA.INV 関数

BETA.INV 関数は、ベータ分布の累積分布関数の逆関数値を返します。

確率が与えられたときに、その確率に対応する値を求めます。

関数の構文

BETA.INV(確率, α, β, [A], [B])

確率：ベータ分布に関連付けられた確率を指定します (0～1)。
α, β：分布のパラメーターを指定します。
[A], [B]：分布の下限と上限を指定します。省略可能です。

関数の使用例

プロジェクトが 95% の確率で完了するためには、何日を完了期限として設定すればよいでしょうか？

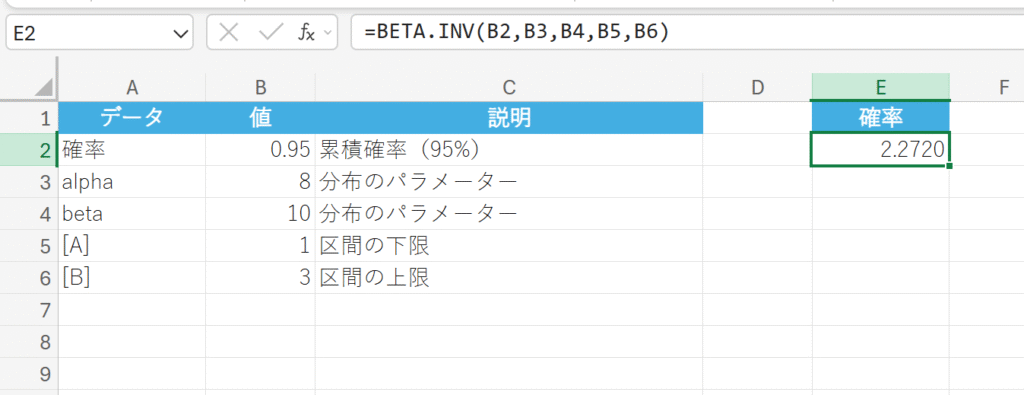
解説

計算結果の約 2.27 は、プロジェクトが 95% の確率で完了するために必要な日数が約 2.27日であることを示しています。プロジェクトマネージャーは、この値を基に現実的な完了期限を設定できます。

13. BINOM.DIST 関数

BINOM.DIST 関数は、二項分布の確率を返します。

二項分布は、「成功」か「失敗」のどちらかしかない試行を繰り返すときに、特定の回数の成功が発生する確率を計算するために使われます（例：コインを10回投げて、表が7回出る確率）。

関数の構文

BINOM.DIST(成功数, 試行回数, 成功率, 累積)

成功数：成功の回数を指定します。
試行回数：独立試行の回数を指定します。
成功率：1 回の試行における成功の確率を指定します。
累積：論理値で、TRUE（累積確率）またはFALSE（単独の確率）を指定します。

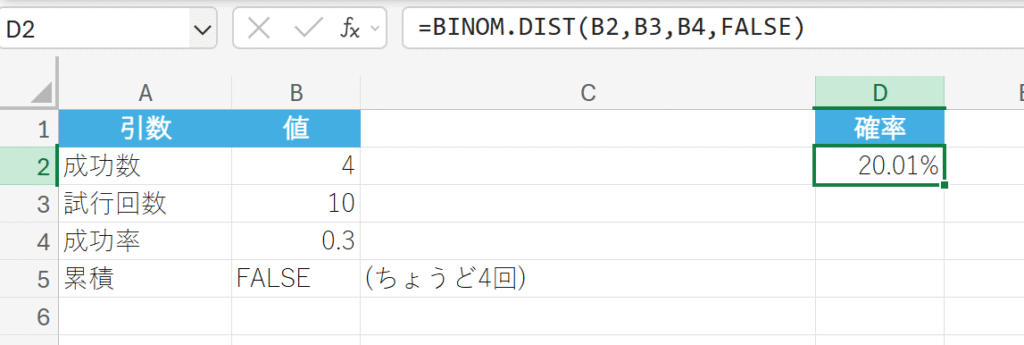
関数の使用例

顧客10人のうち、ちょうど4人が「購入する」確率を求めなさい。

14. BINOM.DIST.RANGE 関数

BINOM.DIST.RANGE 関数は、二項分布の確率を計算します。BINOM.DISTと異なり、成功回数の範囲を指定して計算することができます。

関数の構文

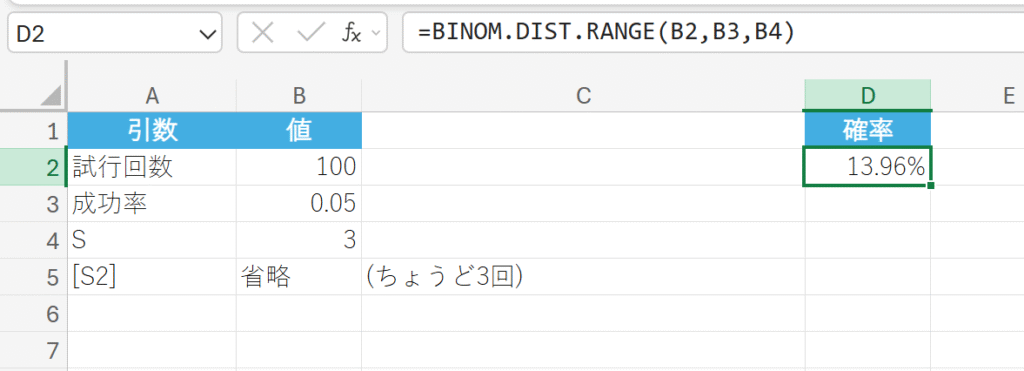
BINOM.DIST.RANGE(試行回数, 成功率, S, [S2])

試行回数：独立試行の回数を指定します。
成功率：1 回の試行における成功の確率を指定します。
S：成功の回数の下限を指定します。
[S2]：成功の回数の上限を指定します。省略すると、成功の回数が S である確率を返します。

関数の使用例

ある製造工程において、製品が不良品となる確率は 5% （0.05）であるとします。ランダムに選んだ製品 100 個を試行回数とします。製品 100 個のうち、ちょうど 3 個が不良品である確率を求めなさい。

15. BINOM.INV 関数

BINOM.INV 関数は、二項分布の累積確率の最大値を返します。

ある確率（基準 α）以下の累積確率となるような最小の成功回数 x を求めるときに使います。例えば、「少なくとも90%の確率で達成できる最小の成功回数は何回か」を知りたい場合に有効です。

関数の構文

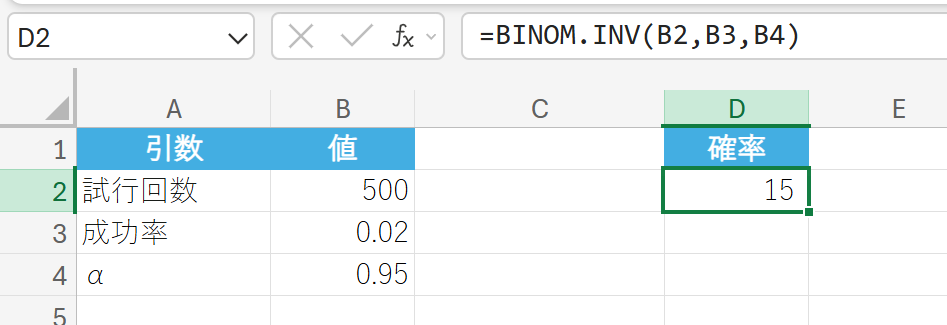
BINOM.INV(試行回数, 成功率, α)

試行回数：独立試行の回数を指定します。
成功率：1 回の試行における成功の確率を指定します。
α：基準となる確率（累積確率）を指定します (0～1)。

関数の使用例

成功率 30% の試行を 10 回行ったとき、累積確率が 95% を超えない最大の成功回数を求めます。95% の確率（α=0.95）で「不良品の数」が収まる、最大の不良品数は何個ですか？（言い換えれば、「不良品の数が x 個以下である累積確率が 95% を超える」ために必要な最小の不良品数 x は何個ですか？）

16. CHISQ.DIST 関数

CHISQ.DIST 関数は、カイ二乗分布の値を返します。

カイ二乗分布は、主に分散の推定や独立性の検定に使われる分布です。

関数の構文

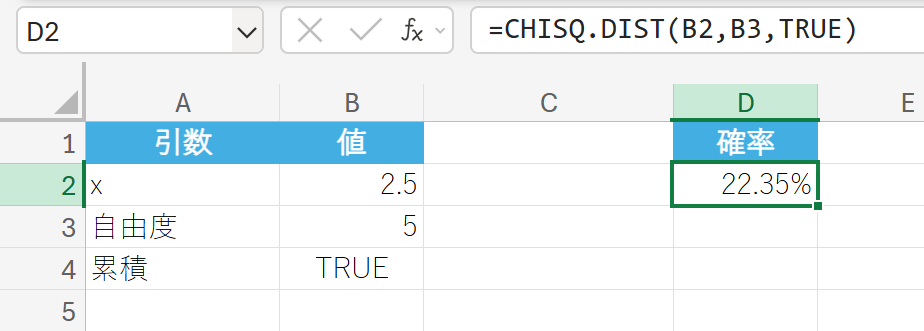
CHISQ.DIST(x, 自由度, 累積)

x：分布を評価する値を指定します。
自由度：分布の自由度を指定します。
累積：論理値で、TRUE（累積分布関数）またはFALSE（確率密度関数）を指定します。

関数の使用例

統計的検定を行った結果、χ2 統計量として 2.5 が得られ、その検定の自由度が 5 であるとします。χ2 統計量が 2.5 以下になる確率（累積確率）はいくつですか？

17. CHISQ.DIST.RT 関数

CHISQ.DIST.RT 関数は、カイ二乗分布の右側確率を返します。

検定でよく使われる関数で、指定された値 x よりも大きい値が出る確率を求めます。

関数の構文

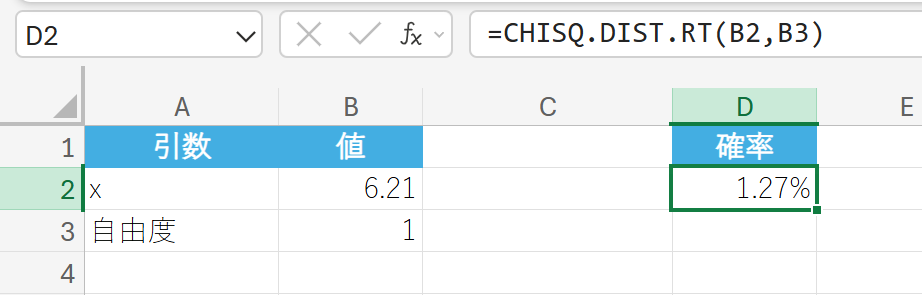
CHISQ.DIST.RT(x, 自由度)

x：分布を評価する値を指定します。
自由度：分布の自由度を指定します。

関数の使用例

あるアンケート調査で、性別と商品Aの購入意向に関連があるかを調べるためにカイ二乗検定を行いました。検定の結果、以下の値が得られました。

χ2 統計量（x）: 6.21
自由度: 1 （クロス集計表が2行2列の場合、(2−1)×(2−1)=1）

χ2 統計量が 6.21 以上になる確率（P値）はいくつですか？

18. CHISQ.INV 関数

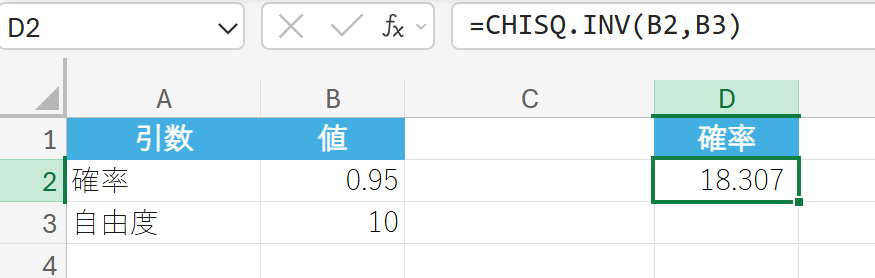
CHISQ.INV 関数は、カイ二乗分布の累積分布関数の逆関数値を返します。

与えられた累積確率に対応するカイ二乗値 x を求めます。

関数の構文

CHISQ.INV(確率, 自由度)

確率：カイ二乗分布に関連付けられた累積確率を指定します (0～1)。
自由度：分布の自由度を指定します。

関数の使用例

あるカイ二乗分布について、自由度が 10 であるとします。この分布の累積確率（左側確率）が 0.95 となる χ2 値はいくつですか？

19. CHISQ.INV.RT 関数

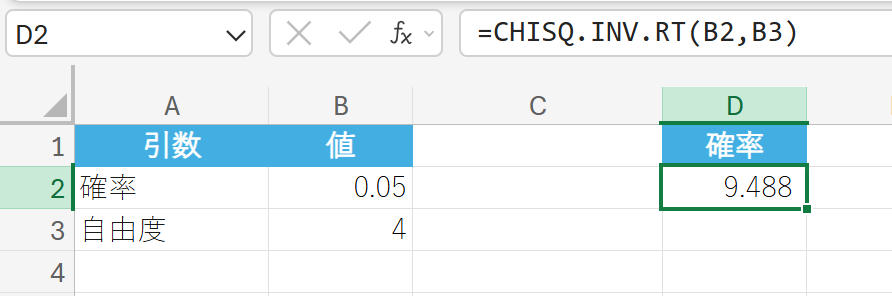
CHISQ.INV.RT 関数は、カイ二乗分布の右側確率の逆関数値を返します。

検定で使われる関数で、与えられた右側確率（有意水準 α）に対応するカイ二乗値 x を求めます。

関数の構文

CHISQ.INV.RT(確率, 自由度)

確率：カイ二乗分布に関連付けられた右側確率を指定します (0～1)。
自由度：分布の自由度を指定します。

関数の使用例

カイ二乗検定を行う際、有意水準を 5% と設定し、自由度が 4 であるとします。このとき、帰無仮説を棄却するための棄却限界値（χ2 値）はいくつですか？

20. CHISQ.TEST 関数

CHISQ.TEST 関数は、独立性のカイ二乗検定の結果（P 値）を返します。

2つのカテゴリ変数（例：性別と購入意向）の間に統計的に有意な関連性があるかどうかを調べるために使われます。

関数の構文

CHISQ.TEST(実測値の範囲, 期待値の範囲)

実測値の範囲：観測された頻度を含むセル範囲を指定します。
期待値の範囲：期待される頻度を含むセル範囲を指定します。

関数の使用例

商品の色の好みの適合度検定してみましょう。

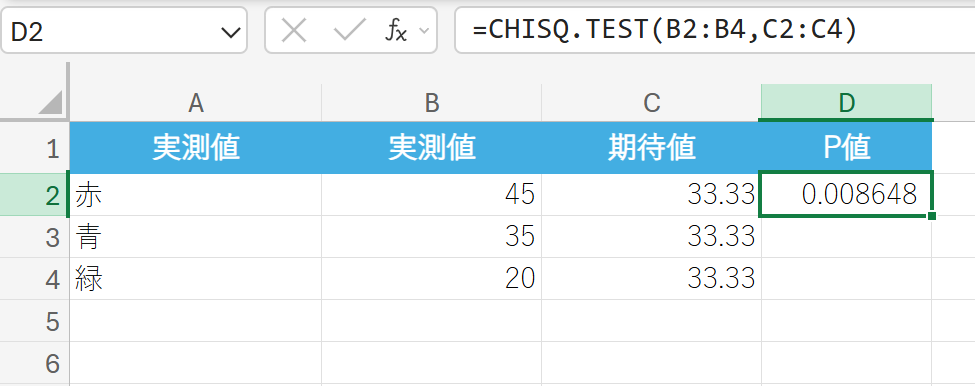
解説

p値 (0.0055) が有意水準 (0.05) より小さいため、帰無仮説を棄却します。これは、「色の好みが均等に分かれる」という仮定は間違っており、観測された色の分布（45:35:20）は偶然とは言えないほど、理論上の均等な分布 (33.33:33.33:33.33) と異なっていることを意味します。つまり、消費者の色には有意な偏り（好み）があると判断できます。

21. CONFIDENCE.NORM 関数

CONFIDENCE.NORM 関数は、正規分布の母平均に対する信頼区間の半値を返します。

母集団の標準偏差が既知の場合に、標本平均がどの程度の範囲で母平均を推定できるか（信頼区間の幅）を計算するために使われます。

関数の構文

CONFIDENCE.NORM(α, 標準偏差, 標本サイズ)

α (アルファ)：有意水準を指定します。信頼度 95% の場合は 1 – 0.95 = 0.05 となります。
標準偏差：母集団の標準偏差を指定します。
標本サイズ：標本の観測値の個数を指定します。

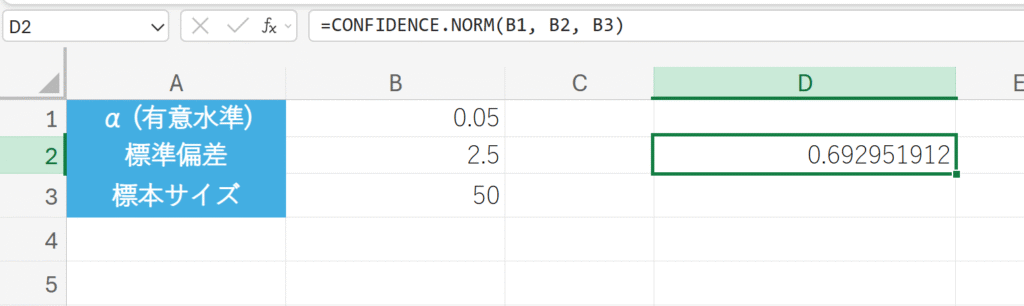
関数の使用例

信頼水準 95% (α=0.05)、母標準偏差 2.5、標本サイズ 50 のデータがある場合の信頼区間の半値（誤差の許容範囲）を求めます。

22. CONFIDENCE.T 関数

CONFIDENCE.T 関数は、スチューデントの t 分布を使用して母集団の平均の信頼区間の半値を返します。

母集団の標準偏差が未知の場合や、標本サイズが小さい場合に、より正確な信頼区間を推定するために使われます。

関数の構文

CONFIDENCE.T(α, 標準偏差, 標本サイズ)

α (アルファ)：有意水準を指定します。信頼度 95% の場合は 0.05 となります。
標準偏差：標本の標準偏差を指定します。
標本サイズ：標本の観測値の個数を指定します。

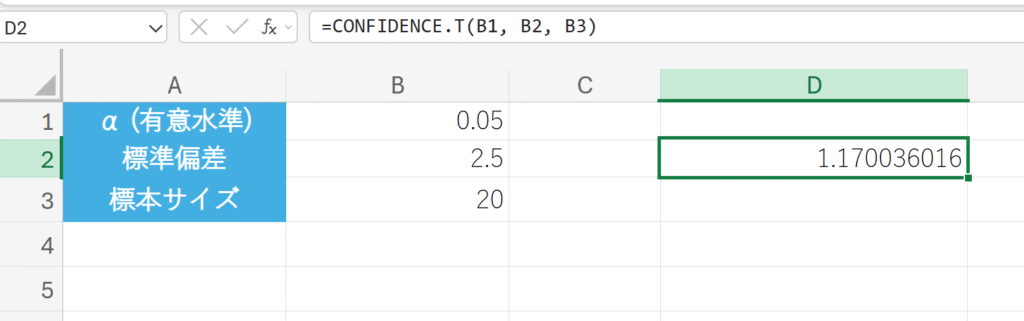
関数の使用例

信頼水準 95% (α=0.05)、標本標準偏差 2.5、標本サイズ 20 のデータがある場合の信頼区間の半値を求めます。

23. CORREL 関数

CORREL 関数は、2 つのデータセット間の相関係数を返します。

相関係数は、2つの変数（例：広告費と売上）がどれだけ強い線形の関係にあるかを示す指標で、−1 から +1 の値をとります。+1 に近いほど強い正の相関（一方が増えればもう一方も増える）、−1 に近いほど強い負の相関（一方が増えればもう一方が減る）があることを示します。

関数の構文

CORREL(配列1, 配列2)

配列1：第 1 のデータセットに対応するセル範囲を指定します。
配列2：第 2 のデータセットに対応するセル範囲を指定します。

関数の使用例

広告費とそれに対応する売上データの間の相関係数を求め、関連性の強さを調べます。

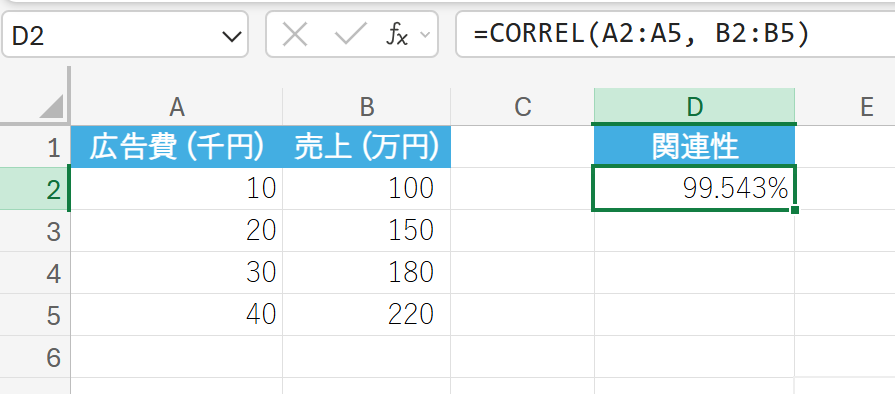
解説

1 に非常に近く、広告費と売上には非常に強い正の相関があることがわかります。

24. COVARIANCE.P 関数

COVARIANCE.P 関数は、2 つのデータセット間の母集団共分散を返します。

共分散は、2つの変数が一緒に変動する度合いを示し、その結果は単位の影響を受けるため、相関係数よりも解釈が難しいですが、回帰分析の基礎となります。これは母集団全体の共分散を計算します。

関数の構文

COVARIANCE.P(配列1, 配列2)

配列1：第 1 のデータセットに対応するセル範囲を指定します。
配列2：第 2 のデータセットに対応するセル範囲を指定します。

関数の使用例

上記と同じ広告費と売上データ（これを母集団全体と仮定）の共分散を求めます。

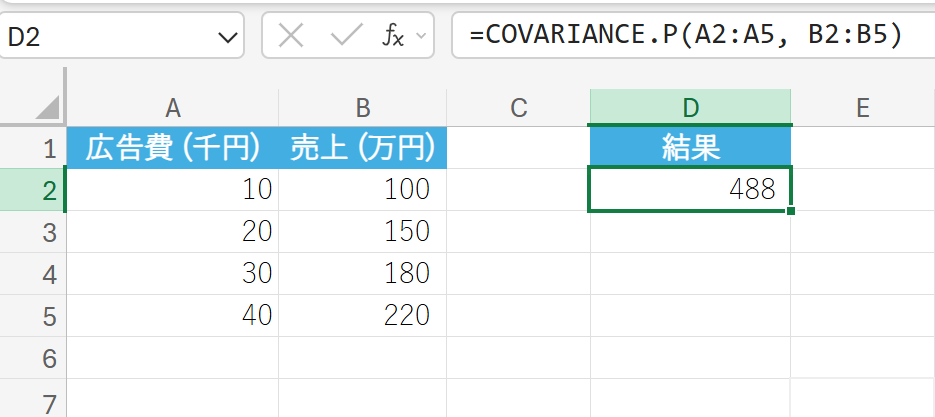
解説

値が正であるため、正の相関があることがわかります。

25. COVARIANCE.S 関数

COVARIANCE.S 関数は、2 つのデータセット間の標本共分散を返します。

計算されるのは COVARIANCE.P と同じ共分散ですが、これはデータが母集団の標本であると仮定して計算されます。一般的に、手元のデータが母集団の一部である場合、こちらを使用します。

関数の構文

COVARIANCE.S(配列1, 配列2)

配列1：第 1 のデータセットに対応するセル範囲を指定します。
配列2：第 2 のデータセットに対応するセル範囲を指定します。

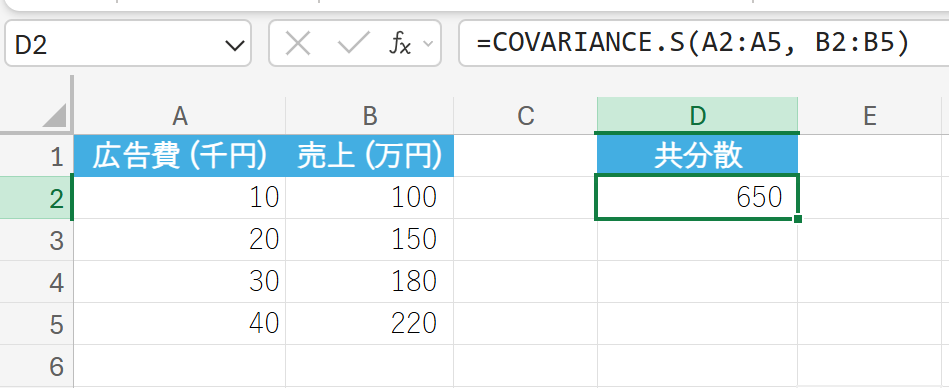
関数の使用例

上記と同じ広告費と売上データ（これを標本と仮定）の共分散を求めます。

26. DEVSQ 関数

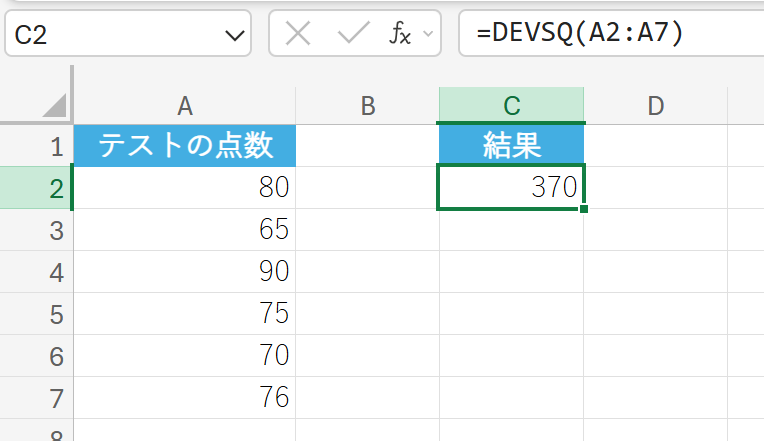
DEVSQ 関数は、標本の平均からの偏差の平方和を返します。

分散や標準偏差を計算する際の基礎となる値です。各データから平均を引いた値（偏差）を二乗し、それらをすべて合計した値になります。

関数の構文

DEVSQ(数値1, [数値2], …)

数値1, [数値2], …：偏差の平方和を求めたいデータポイントに対応する引数を指定します。

関数の使用例

あるテストの点数データの、平均からの偏差の平方和を求めます。

27. EXPON.DIST 関数

EXPON.DIST 関数は、指数分布の値を返します。

指数分布は、ポアソン過程（発生率が一定の事象）における次の事象が発生するまでの時間をモデル化するのに使われます（例：コールセンターで次の電話がかかってくるまでの確率）。

関数の構文

EXPON.DIST(x, λ, 累積)

x：分布を評価する値を指定します (事象が発生するまでの時間)。
λ (ラムダ)：パラメーター値 (事象発生率) を指定します。
累積：論理値で、TRUE（累積分布関数）またはFALSE（確率密度関数）を指定します。

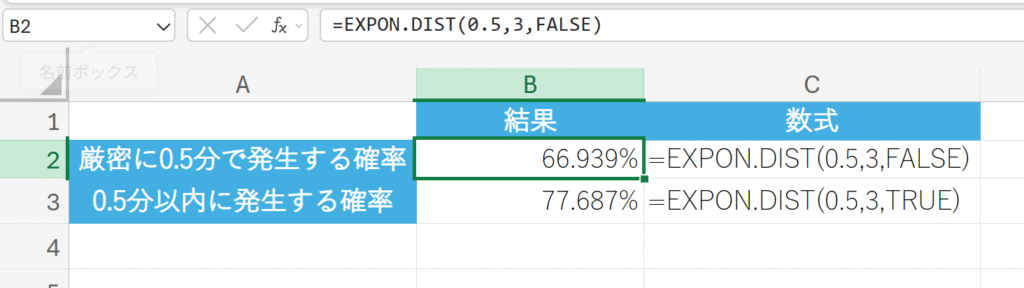
関数の使用例

あるコールセンターには、平均して1分あたり3件の電話がかかってきます。この情報（λ=3）を基に、以下の確率を計算しなさい。
次の電話がかかってくるまでに、0.5分以内に済む確率（累積確率）
次の電話がかかってくるまでに、厳密に0.5分かかる確率（点確率）

28. F.DIST 関数

F.DIST 関数は、F 分布の値を返します。

F 分布は、主に分散の比率を比較する F 検定に使用されます。

関数の構文

F.DIST(x, 自由度1, 自由度2, 累積)

x：分布を評価する値を指定します。
自由度1：分子の自由度を指定します。
自由度2：分母の自由度を指定します。
累積：論理値で、TRUE（累積分布関数）またはFALSE（確率密度関数）を指定します。

関数の使用例

あるデータ分析で、F統計量（F値）が 4.5 と計算され、そのF値の計算に使われたデータの自由度が以下のように設定されました。

F値 (x)： 4.5
分子の自由度（自由度1）： 5
分母の自由度（自由度2）： 15

このF値 4.5 の累積確率（4.5 以下の確率）を計算しなさい。

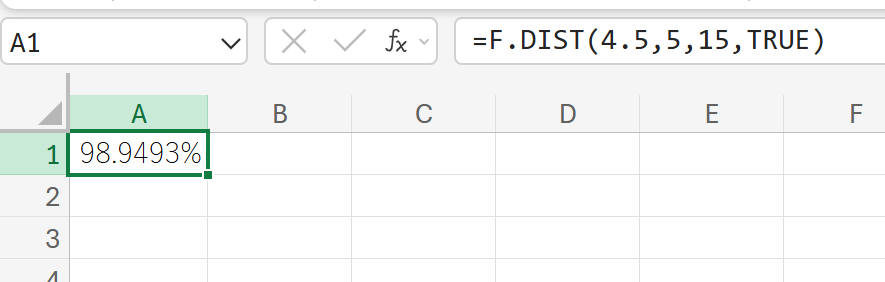
解説

F分布において、F値が 4.5 以下になる確率が98.94%であることを示します。

29. F.DIST.RT 関数

F.DIST.RT 関数は、F 分布の右側確率を返します。

これは F 検定で P 値を計算する際に使われ、F 分布の右側（大きい方）の確率を求めます。

関数の構文

F.DIST.RT(x, 自由度1, 自由度2)

x：分布を評価する値を指定します。
自由度1：分子の自由度を指定します。
自由度2：分母の自由度を指定します。

関数の使用例

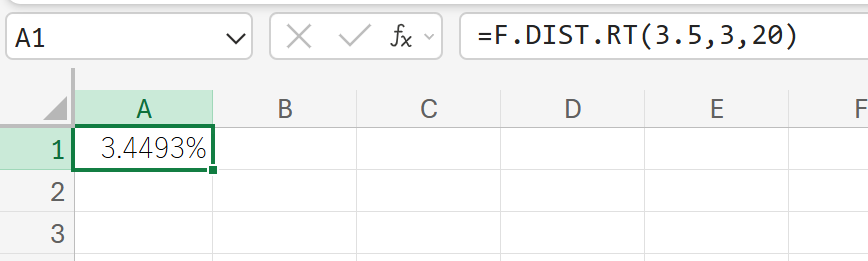
あるデータセットにおいて、分散分析（ANOVA）を実行した結果、以下の値が得られました。

F統計量（F値）： 3.5
分子の自由度（グループ間の自由度）： 3
分母の自由度（残差の自由度）： 20

このF値 3.5 に対応するp値（上側確率）を計算しなさい。

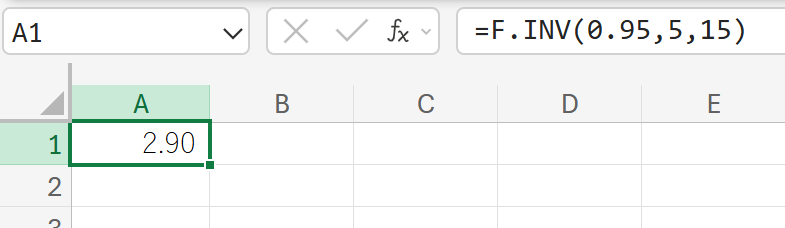
30. F.INV 関数

F.INV 関数は、F 分布の累積分布関数の逆関数値を返します。

与えられた累積確率に対応する F 値を求めます。

関数の構文

F.INV(確率, 自由度1, 自由度2)

確率：F 分布に関連付けられた累積確率を指定します (0～1)。
自由度1, 自由度2：それぞれの自由度を指定します。

関数の使用例

有意水準 α=0.05 で、以下の自由度を持つF検定を行うことになりました。

有意水準 (α)： 0.05
分子の自由度（自由度1）： 5
分母の自由度（自由度2）： 15

この検定において、片側検定の臨界F値を計算しなさい。

31. F.INV.RT 関数

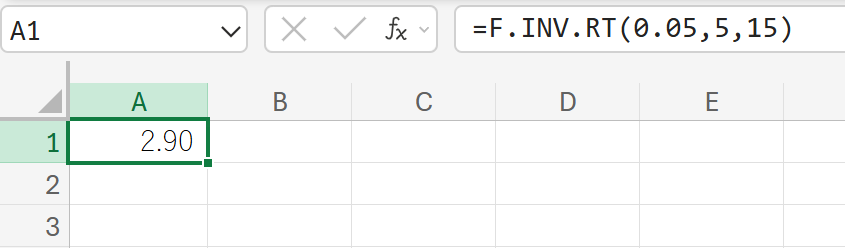
F.INV.RT 関数は、F 分布の右側確率の逆関数値を返します。

F 検定の棄却域を決めるクリティカル値を計算するために使われます。与えられた有意水準（右側確率）に対応する F 値を求めます。

関数の構文

F.INV.RT(確率, 自由度1, 自由度2)

確率：F 分布に関連付けられた右側確率（有意水準 α）を指定します (0～1)。
自由度1, 自由度2：それぞれの自由度を指定します。

関数の使用例

有意水準 α=0.05 で、以下の自由度を持つF検定を行うことになりました。

有意水準 (α)： 0.05
分子の自由度（自由度1）： 5
分母の自由度（自由度2）： 15

この検定において、棄却域の境界となる臨界F値を計算しなさい。

32. F.TEST 関数

F.TEST 関数は、F 検定の結果（P 値）を返します。

2つの標本の分散に統計的に有意な差があるかどうかを検定するために使われます。

関数の構文

F.TEST(配列1, 配列2)

配列1：第 1 のデータセットに対応するセル範囲を指定します。
配列2：第 2 のデータセットに対応するセル範囲を指定します。

関数の使用例

2つの異なるグループのテストの点数データ（分散）に差があるか検定します。

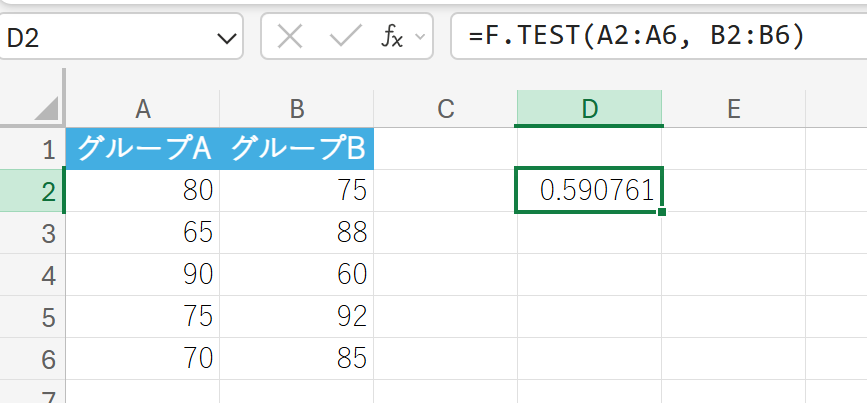
解説

P値が求められます。この値が有意水準（0.05など）より大きいため、このデータでは分散に有意な差があるとは言えません。

33. FISHER 関数

FISHER 関数は、フィッシャー変換を返します。

フィッシャー変換は、相関係数を正規分布に従うように変換するために使われます。特に、相関係数に統計的検定を行う際や、複数の相関係数の平均を計算する際に役立ちます。

関数の構文

FISHER(r)

r：相関係数を指定します (-1 から 1 の範囲)。

関数の使用例

相関係数 r=0.8 をフィッシャー変換します。

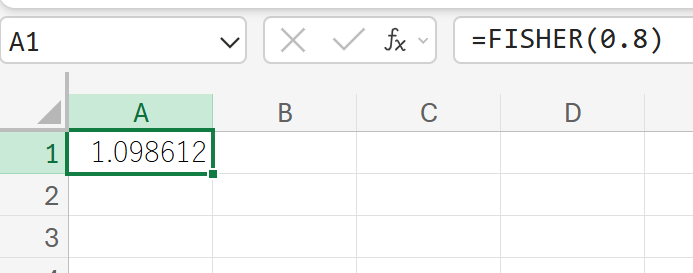
34. FISHERINV 関数

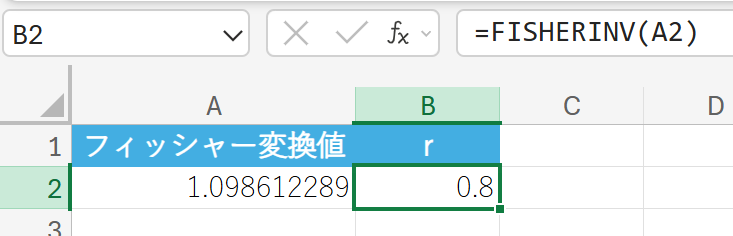
FISHERINV 関数は、フィッシャー逆変換を返します。

フィッシャー変換された値（z 値）を元の相関係数 r に戻すために使われます。

関数の構文

FISHERINV(y)

y：フィッシャー変換した値を指定します。

関数の使用例

フィッシャー変換値 z=1.0986 を、元の相関係数 r に戻します。

35. FORECAST.LINEAR 関数

FORECAST.LINEAR 関数は、既存の値に基づいて将来の値を予測します。

線形回帰（データがほぼ直線状に並ぶ傾向）を用いて、過去のデータに基づいた将来の予測値を計算するために使われます。

関数の構文

FORECAST.LINEAR(X, 既知の y, 既知の x)

X：将来の予測値を求める x 座標（独立変数）の値を指定します。
既知の y：既知の y 座標（従属変数）のデータ群を指定します。
既知の x：既知の x 座標（独立変数）のデータ群を指定します。

関数の使用例

過去の月ごとの広告費と売上のデータに基づき、広告費が 50 万円だった場合の売上を予測します。

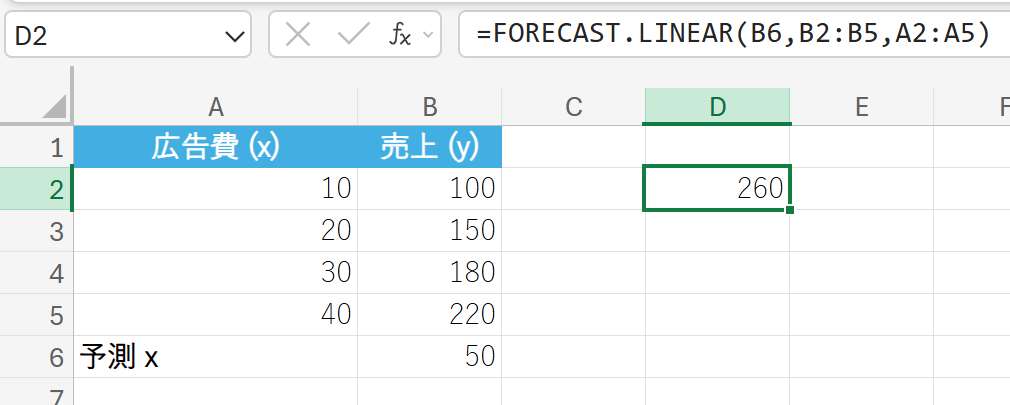
解説

広告費 50 万円の場合、売上は 258 万円と予測されます。

36. FREQUENCY 関数

FREQUENCY 関数は、値の頻度分布を垂直配列で計算します。

データが特定の区間（階級）にいくつ含まれているかを数える際に使用します。結果は複数のセルにわたる配列として返されるため、配列数式として入力する必要があります。

関数の構文

FREQUENCY(データ配列, 区間配列)

データ配列：度数を求めるデータセットを含む配列またはセル範囲を指定します。
区間配列：データをグループ化する区間（階級の上限）を含む配列またはセル範囲を指定します。

関数の使用例

テストの点数データを 60 点以下、 70 点以下、 80 点以下…という区間でグループ化し、各区間に何人いるか数えます。

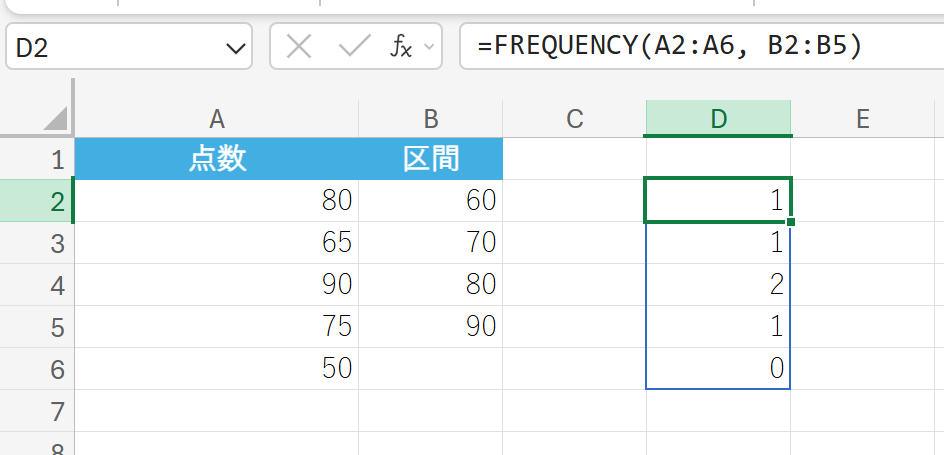
解説

50点 (60点以下)、65点 (70点以下)、75点 (80点以下)、80点 (90点以下)、90点 (90点超) の度数が順に返されます。

37. GAMMA 関数

GAMMA 関数は、ガンマ関数値を返します。

ガンマ関数は階乗の概念を実数に拡張したもので、確率分布の計算によく使われる特殊関数です。

関数の構文

GAMMA(x)

x：計算する値を指定します。x > 0 である必要があります。

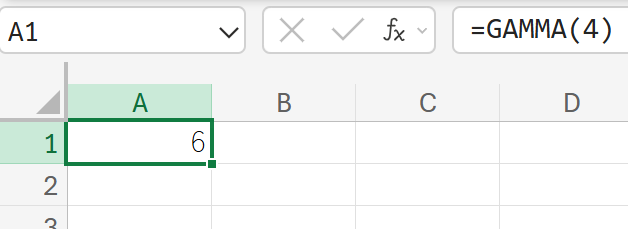
関数の使用例

GAMMA(4) の値を求めます。GAMMA(n)=(n−1)! の関係があるため、GAMMA(4)=3!=6 となります。

38. GAMMA.DIST 関数

GAMMA.DIST 関数は、ガンマ分布の値を返します。

ガンマ分布は、待ち時間のモデル化など、確率変数が正の値を取る事象に使われる連続確率分布です。

関数の構文

GAMMA.DIST(x, α, β, 累積)

x：分布を評価する値を指定します。
α (アルファ), β (ベータ)：分布のパラメーターを指定します。
累積：論理値で、TRUE（累積分布関数）またはFALSE（確率密度関数）を指定します。

関数の使用例

ある高性能な製造機械の故障時間（稼働時間）が、以下のパラメーターを持つガンマ分布に従うと仮定します。

形状パラメーター (α)： 2.0
尺度パラメーター (β)： 3.0

このとき、以下の確率を計算しなさい。
稼働時間が5時間以下で故障する確率
稼働時間が厳密に5時間で故障する確率密度

39. GAMMA.INV 関数

GAMMA.INV 関数は、ガンマ分布の累積分布関数の逆関数値を返します。

与えられた累積確率に対応する x の値を求めます。

関数の構文

GAMMA.INV(確率, α, β)

確率：ガンマ分布に関連付けられた累積確率を指定します (0～1)。
α, β：分布のパラメーターを指定します。

関数の使用例

α=9、β=2 のガンマ分布において、累積確率が 90% となる x の値を求めます。

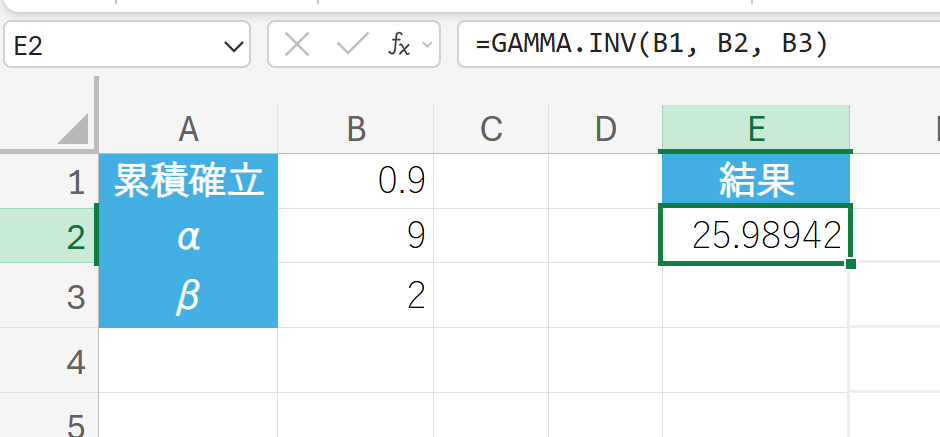
40. GAMMALN 関数

GAMMALN 関数は、ガンマ関数の自然対数を返します。

大きな数の計算でオーバーフローを防ぐために、GAMMA(x) ではなく、ln(GAMMA(x)) を計算します。

関数の構文

GAMMALN(x)

x：計算する値を指定します (x > 0 である必要があります)。

関数の使用例

GAMMALN(4) の値を求めます。これは ln(3!)=ln(6) に等しいです。

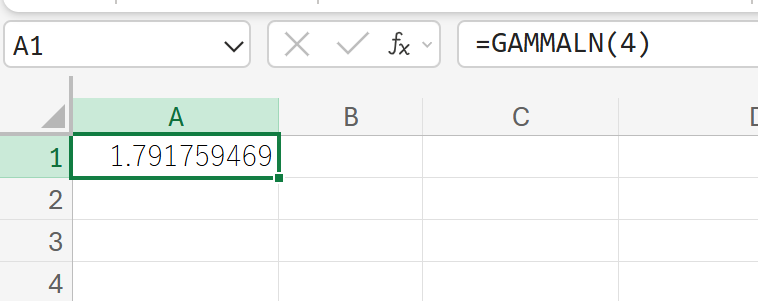
41. GAMMALN.PRECISE 関数

GAMMALN.PRECISE 関数は、ガンマ関数の自然対数を返します。

GAMMALN 関数と同じ計算を行いますが、GAMMALN.PRECISE は新しいバージョン（Excel 2010以降）で用意された関数で、より精度の高い計算を行うことができます。

関数の構文

GAMMALN.PRECISE(x)

x：計算する値を指定します (x > 0 である必要があります)。

関数の使用例

GAMMALN.PRECISE(4) の値を求めます。

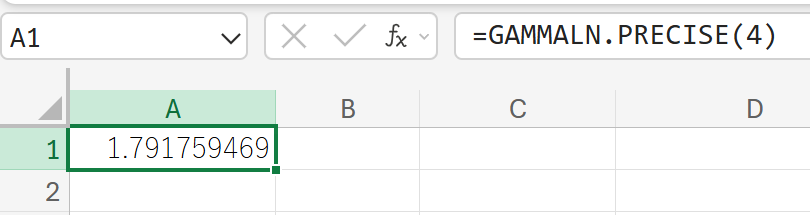
42. GAUSS 関数

GAUSS 関数は、標準正規分布の累積分布関数の値から 0.5 を引いた値を返します。

標準正規分布（平均 μ=0、標準偏差 σ=1 の正規分布）の累積分布関数 NORM.S.DIST(Z, TRUE) から 0.5 を引いた値に等しく、平均から z 値までの累積確率を求めます。

関数の構文

GAUSS(Z)

Z：正規分布を標準正規分布に変換した z 値を指定します。

関数の使用例

z 値が 1.5 の場合の、平均から z=1.5 までの累積確率を求めます。

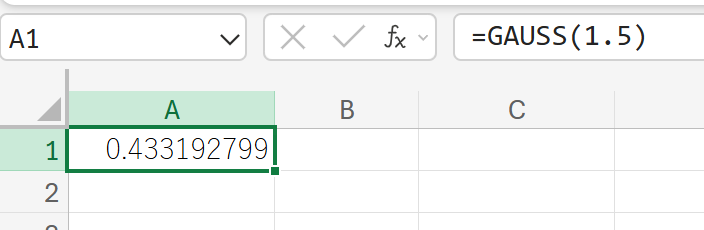
43. GEOMEAN 関数

GEOMEAN 関数は、相対成長率を計算する際の幾何平均を返します。

特に、時間と共に変動する成長率や、資産の平均リターンを計算する際など、積の平均を求めたい場合に使用されます。

関数の構文

GEOMEAN(数値1, [数値2], …)

数値1, [数値2], …：幾何平均を求めたい 1〜255 個の数値、または数値を含む配列やセル範囲を指定します。

関数の使用例

4期間における商品の販売成長率データ（1.1倍、1.2倍、1.05倍、1.3倍）の幾何平均成長率を求めます。

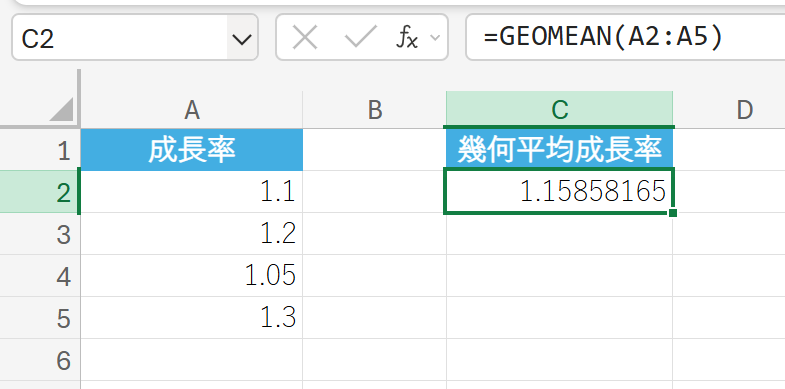
解説

4期間の平均成長率が約 1.158倍であることを示します。

44. GROWTH 関数

GROWTH 関数は、指数曲線に沿って成長率を予測します。

既存の x および y の値に基づいて、指数関数 y=b⋅mx に沿って新しい x の値に対する y の予測値を計算します。

関数の構文

GROWTH(既知の y, [既知の x], [新しい x], [定数])

既知の y, [既知の x]：既知のデータセットを指定します。
[新しい x]：予測値を計算したい x の値を指定します。省略すると、既知の x を使用します。
[定数]：論理値で、TRUE（定数 b を計算）またはFALSE（定数 b を 1 に強制）を指定します。

関数の使用例

過去4年間の売上データに基づき、5年目の売上を指数的に予測します。

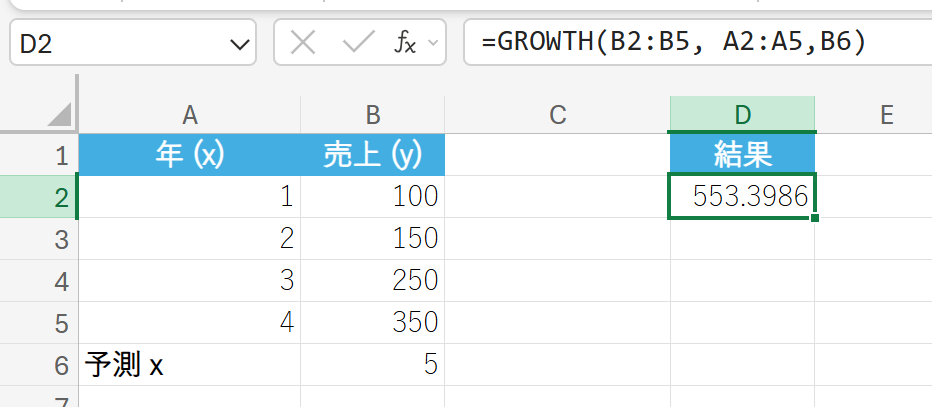
解説

5年目の売上が約 511.23 と指数的に予測されます。

45. HARMEAN 関数

HARMEAN 関数は、母集団の調和平均を返します。

調和平均は、比率や速度、料金など、逆数の平均が必要な場合に使われます（例：往復の平均速度）。

関数の構文

HARMEAN(数値1, [数値2], …)

数値1, [数値2], …：調和平均を求めたい 1〜255 個の数値、または数値を含む配列やセル範囲を指定します。

関数の使用例

往路時速 10 km、復路時速 20 km の場合の往復の平均速度を調和平均で求めます。

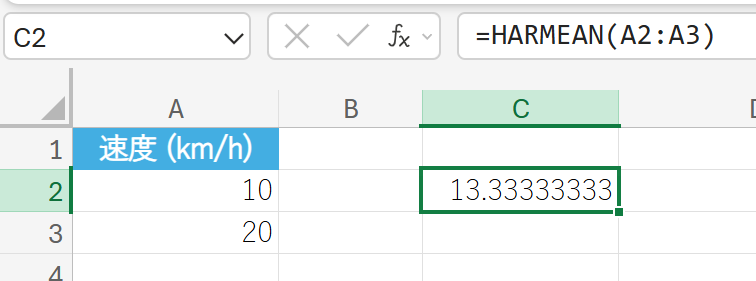
46. HYPGEOM.DIST 関数

HYPGEOM.DIST 関数は、超幾何分布の確率を返します。

超幾何分布は、非復元抽出（一度選んだものは元に戻さない）において、標本中に特定の事象が特定の回数含まれる確率を計算するために使われます（例：箱からトランプを 5 枚引いたとき、その中に A が 2 枚含まれる確率）。

関数の構文

HYPGEOM.DIST(成功数, 標本数, 母集団の成功数, 母集団の大きさ, 累積)

成功数：標本抽出で成功した回数を指定します。
標本数：標本抽出の回数を指定します。
母集団の成功数：母集団全体に含まれる成功の個数を指定します。
母集団の大きさ：母集団全体の個数を指定します。
累積：論理値で、TRUE（累積確率）またはFALSE（単独の確率）を指定します。

関数の使用例

ある製造ロットの製品（母集団）50個の中に、不良品が 5 個含まれています。

このロットから製品を非復元で 10 個抽出するとき、以下の確率を計算しなさい。
抽出した 10 個の中に、不良品が 2 個以下含まれている確率。
抽出した 10 個の中に、不良品がぴったり 2 個含まれている確率。

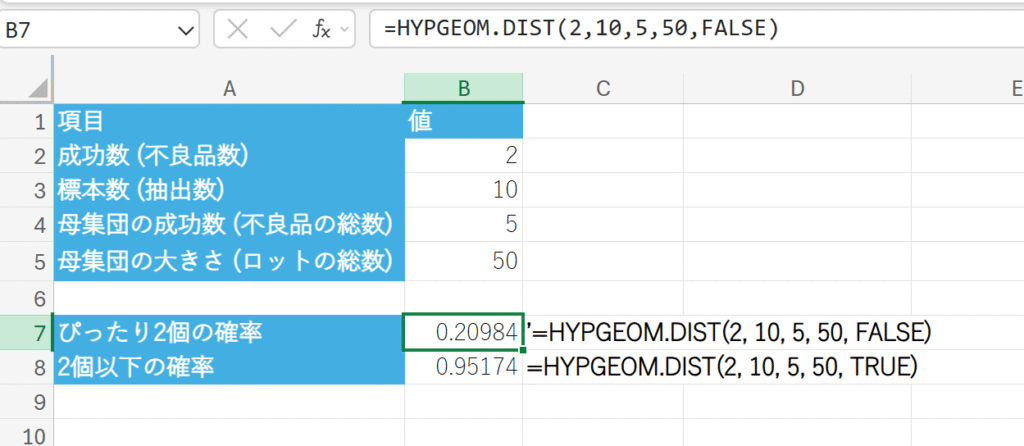
47. INTERCEPT 関数

INTERCEPT 関数は、線形回帰直線の切片を計算します。

線形回帰直線 y=ax+b における y 軸との交点（x=0 のときの y の値、つまり切片 b）を計算します。

関数の構文

INTERCEPT(既知の y, 既知の x)

既知の y, 既知の x：既知のデータセットを指定します。

関数の使用例

広告費と売上のデータに基づき、広告費が 0 万円だった場合の予測売上（切片）を求めます。

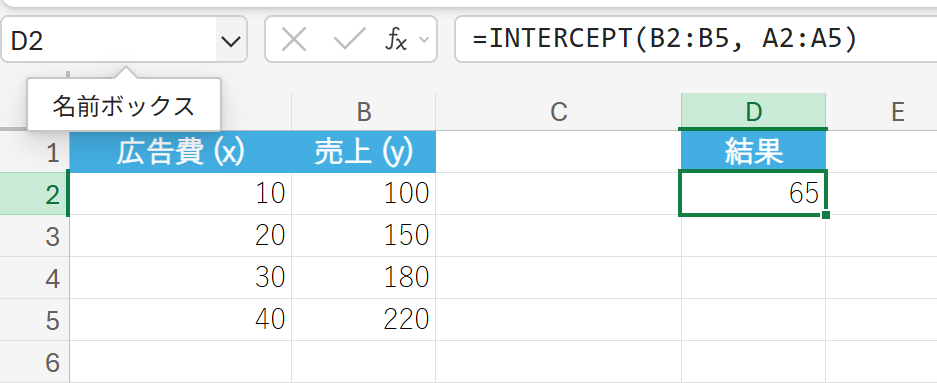
解説

広告費が 0 でも 65 万円の売上が見込めると予測されます。

48. KURT 関数

KURT 関数は、データセットの尖度 (せんど) を返します。

尖度は、データの分布のとがり具合や、裾野の広がり具合を示す指標です。正規分布の尖度は 0 です。正の値であれば正規分布より尖った（裾が重い）分布、負の値であれば正規分布より平らな（裾が軽い）分布であることを示します。

関数の構文

KURT(数値1, [数値2], …)

数値1, [数値2], …：尖度を計算したい 1〜255 個の数値、または数値を含む配列やセル範囲を指定します。

関数の使用例

あるテストの点数データの尖度を求め、分布のとがり具合を調べます。

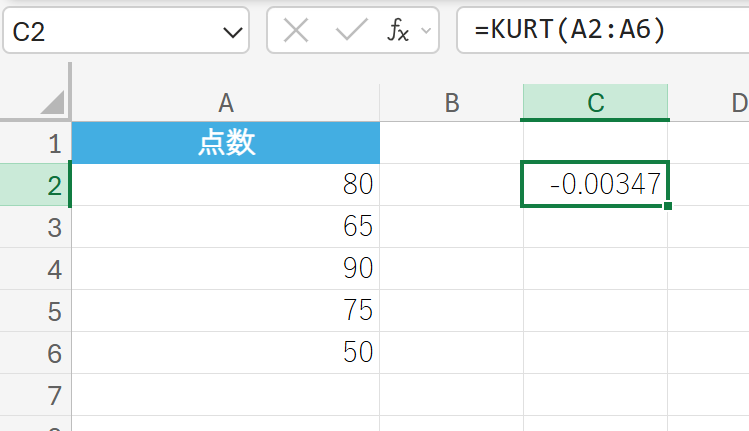
49. LARGE 関数

LARGE 関数は、データセット内の K 番目に大きな値を返します。

最大値 (1 番目に大きな値) や 2 番目に大きな値などを簡単に求めたいときに使います。

関数の構文

LARGE(配列, K)

配列：K 番目に大きな値を求めるデータを含む配列またはセル範囲を指定します。
K：返す順位を指定します (1 は最大値、2 は 2 番目に大きな値)。

関数の使用例

テストの点数データから、2 番目に大きな値（2 番目に高得点の点数）を求めます。

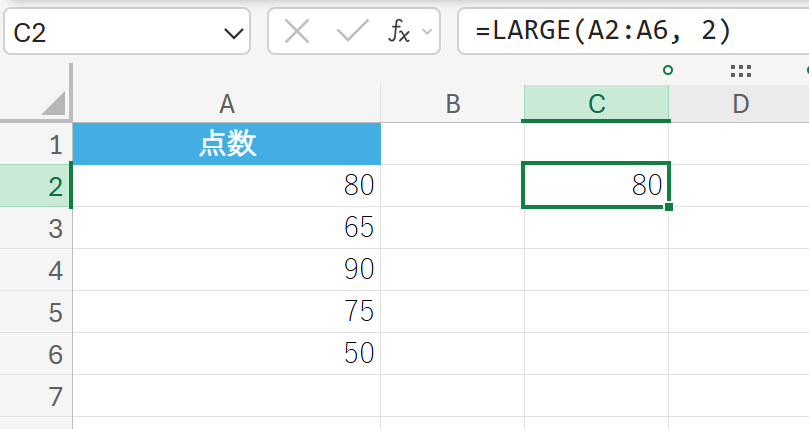
50. LINEST 関数

LINEST 関数は、データの最小二乗法による直線回帰を計算します。

線形回帰 y=ax+b の傾き a と切片 b、および回帰に関する各種統計値（R 二乗値、標準誤差など）を配列で返します。

関数の構文

LINEST(既知の y, [既知の x], [定数], [統計])

既知の y, [既知の x]：既知のデータセットを指定します。
[定数]：論理値で、TRUE（切片 b を計算）またはFALSE（切片 b を 0 に強制）を指定します。
[統計]：論理値で、TRUE（追加の統計値を返す）またはFALSE（傾き a と切片 b のみ返す）を指定します。

関数の使用例

広告費と売上のデータに基づき、傾きと切片を求めます。配列数式として入力する必要があります。

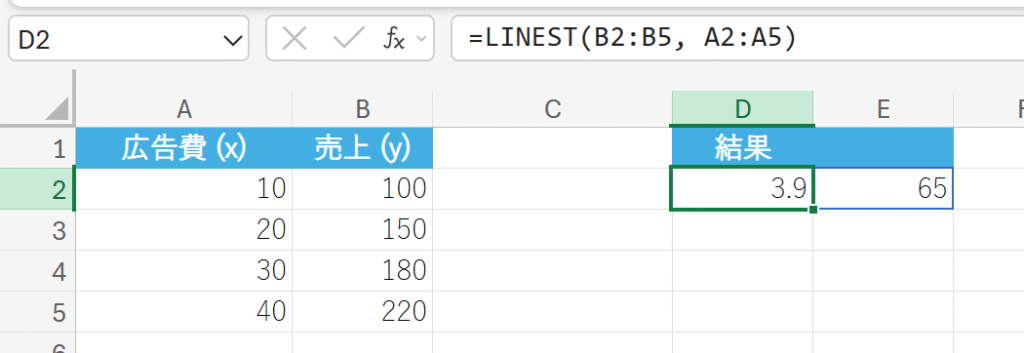
51. LOGEST 関数

LOGEST 関数は、既知のデータを使用して、指数回帰曲線を計算します。

指数回帰 y=b⋅mx の成長率 m と定数 b、および回帰に関する各種統計値を配列で返します。

関数の構文

LOGEST(既知の y, [既知の x], [定数], [統計])

既知の y, [既知の x]：既知のデータセットを指定します。
[定数]：論理値で、TRUE（定数 b を計算）またはFALSE（定数 b を 1 に強制）を指定します。
[統計]：論理値で、TRUE（追加の統計値を返す）またはFALSE（成長率 m と定数 b のみ返す）を指定します。

関数の使用例

過去 4 年間の売上データに基づき、成長率と定数を求めます。配列数式として入力する必要があります。

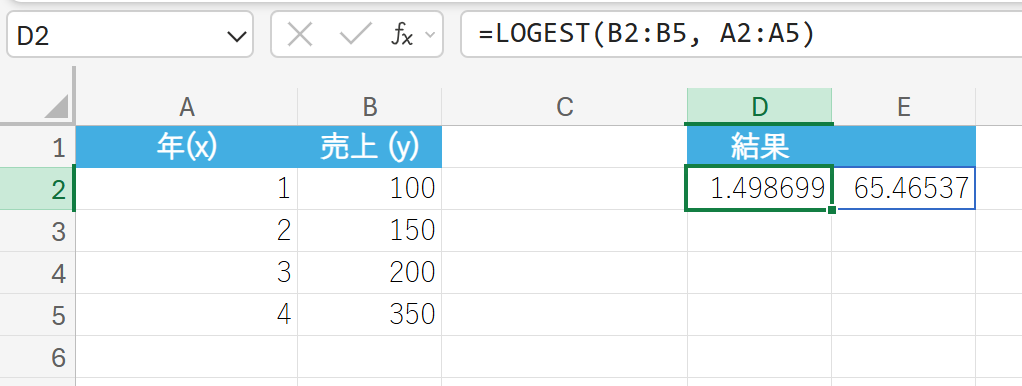
52. LOGNORM.DIST 関数

LOGNORM.DIST 関数は、対数正規分布の累積分布関数または確率密度関数の値を返します。

対数正規分布は、確率変数の対数が正規分布に従う分布で、財務や生物学などで正の値のみをとるデータをモデル化する際に使われます。

関数の構文

LOGNORM.DIST(x, 平均, 標準偏差, 累積)

x：分布を評価する値を指定します。
平均, 標準偏差：対数変換された変数 (ln(x)) の平均と標準偏差を指定します。
累積：論理値で、TRUE（累積分布関数）またはFALSE（確率密度関数）を指定します。

関数の使用例

ある金融資産の価格変動が対数正規分布に従うと仮定します。この分布のパラメーターは、対数変換後の値に基づいて以下のように推定されました。

対数変換後の平均 (μ)： 0.05
対数変換後の標準偏差 (σ)： 0.20

このとき、現在の株価から 10% 上昇した価格（例：現在の価格 P に対し 1.10×P）となる確率を評価したいとします。
ただし、ここでは簡単に特定の時点の株価 x を 1.10 と仮定して、以下の確率を計算しなさい。
株価が厳密に 1.10 となる確率密度
株価が 1.10 以下となる確率

53. LOGNORM.INV 関数

LOGNORM.INV 関数は、対数正規分布の累積分布関数の逆関数値を返します。

与えられた累積確率に対応する x の値を求めます。

関数の構文

LOGNORM.INV(確率, 平均, 標準偏差)

確率：対数正規分布に関連付けられた累積確率を指定します (0～1)。
平均, 標準偏差：対数変換された変数 (ln(x)) の平均と標準偏差を指定します。

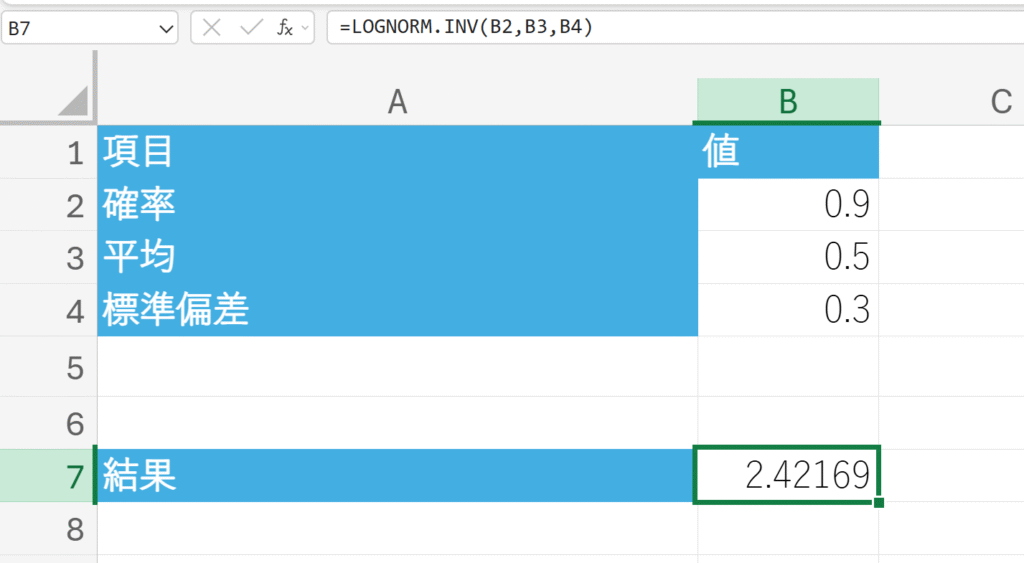
関数の使用例

対数変換されたデータの平均 0.5、標準偏差 0.3 のとき、累積確率が 90% となる x の値を求めます。

54. MAX 関数

MAX 関数は、引数リストの最大値を返します。

セル範囲内の数値の最大値を求めます。文字列、論理値、空白のセルは無視されます。

関数の構文

MAX(数値1, [数値2], …)

数値1, [数値2], …：最大値を求めたい 1〜255 個の数値引数、または数値を含む配列やセル範囲を指定します。

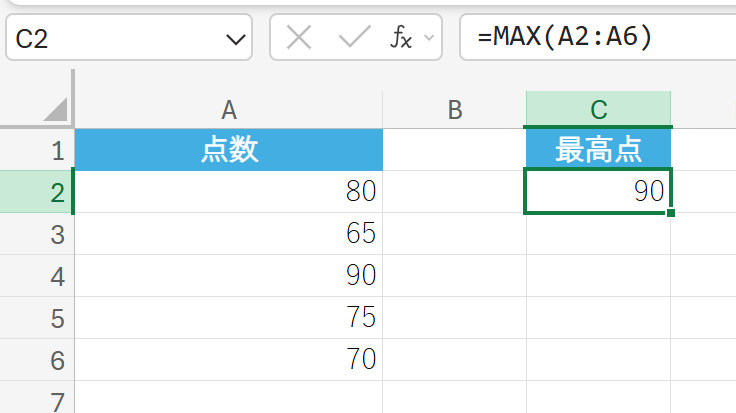
関数の使用例

テストの点数データから、最高得点を求めます。

55. MAXA 関数

MAXA 関数は、引数リストの最大値を返しますが、論理値や文字列も評価の対象とします。

MAX関数との違いは、引数に含まれる文字列を 0 として、論理値の TRUEを 1、FALSEを 0 として計算の対象に含める点です。

関数の構文

MAXA(値1, [値2], …)

値1, [値2], …：最大値を求めたい 1〜255 個の引数、または配列やセル範囲を指定します。

関数の使用例

テストの点数データにボーナス TRUE と欠席 “欠席” のデータを含めて最大値を求めます。

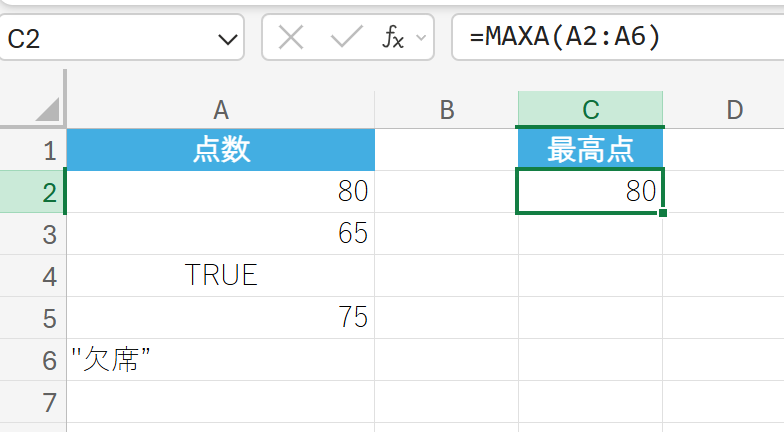
解説

80, 65, 1, 75, 0 のうち最大値は 80 です。

56. MAXIFS 関数

MAXIFS 関数は、複数の条件を満たすセルの中から最大値を返します。

条件付きで最大値を求めたい場合に非常に便利です（例：「関東地方」の「A商品」の最大売上）。

関数の構文

MAXIFS(最大範囲, 範囲1, 条件1, [範囲2, 条件2], …)

最大範囲：最大値を求める実際の数値を含むセル範囲を指定します。
範囲1, 条件1, …：それぞれの条件を適用するセル範囲と条件を指定します。

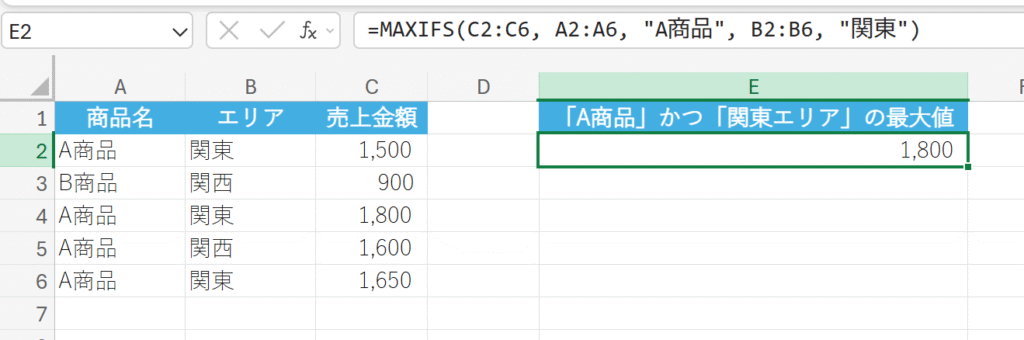
関数の使用例

商品の種類とエリアのデータを使用して、「A商品」かつ「関東エリア」の最大売上を求めます。

57. MEDIAN 関数

MEDIAN 関数は、与えられた数値の中央値を返します。

中央値は、データを昇順または降順に並べたとき、ちょうど真ん中に位置する値です。外れ値（極端に大きな値や小さな値）の影響を受けにくいため、平均値よりもデータの代表値として適している場合があります。

関数の構文

MEDIAN(数値1, [数値2], …)

数値1, [数値2], …：中央値を求めたい 1〜255 個の数値、または数値を含む配列やセル範囲を指定します。

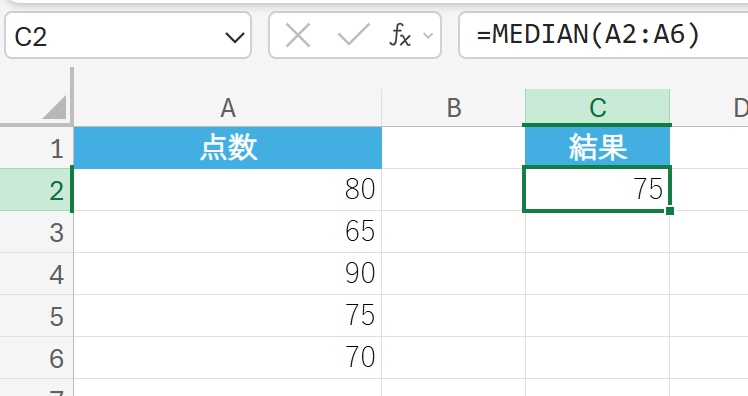
関数の使用例

テストの点数データの中央値を求めます。

58. MIN 関数

MIN 関数は、引数リストの最小値を返します。

セル範囲内の数値の最小値を求めます。文字列、論理値、空白のセルは無視されます。

関数の構文

MIN(数値1, [数値2], …)

数値1, [数値2], …：最小値を求めたい 1〜255 個の数値引数、または数値を含む配列やセル範囲を指定します。

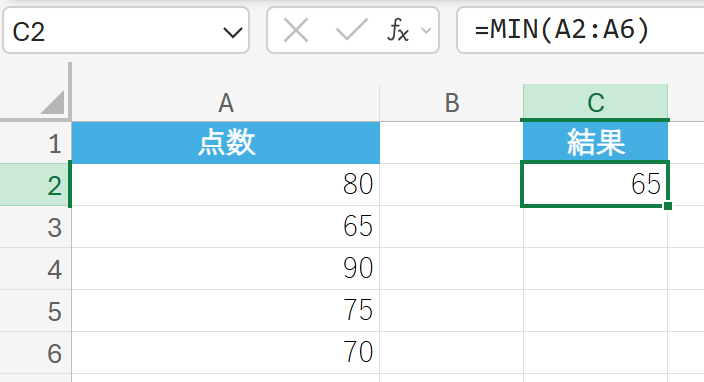
関数の使用例

テストの点数データから、最低得点を求めます。

59. MINA 関数

MINA 関数は、引数リストの最小値を返しますが、論理値や文字列も評価の対象とします。

引数に含まれる文字列を 0 として、論理値の TRUEを 1、FALSEを 0 として計算の対象に含めます。

関数の構文

MINA(値1, [値2], …)

値1, [値2], …：最小値を求めたい 1〜255 個の引数、または配列やセル範囲を指定します。

関数の使用例

テストの点数データに論理値や文字列を含めて最小値を求めます。

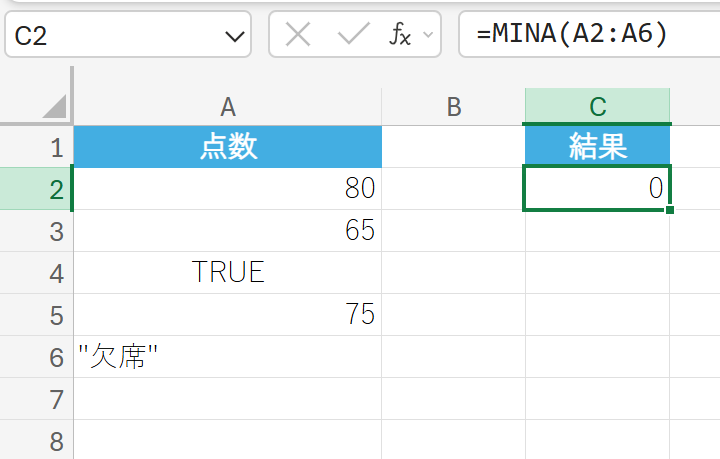
解説

80, 65, 1, 75, 0 のうち最小値は 0 (文字列 “欠席”) です。

60. MINIFS 関数

MINIFS 関数は、複数の条件を満たすセルの中から最小値を返します。

条件付きで最小値を求めたい場合に便利です（例：「東北地方」の「B商品」の最小仕入れ価格）。

関数の構文

MINIFS(最小範囲, 範囲1, 条件1, [範囲2, 条件2], …)

最小範囲：最小値を求める実際の数値を含むセル範囲を指定します。
範囲1, 条件1, …：それぞれの条件を適用するセル範囲と条件を指定します。

関数の使用例

商品の種類とエリアのデータを使用して、「A商品」かつ「関東エリア」の最小売上を求めます。

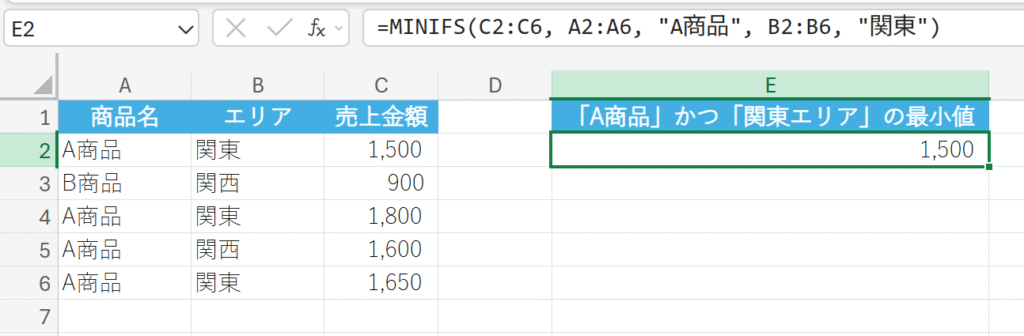
61. MODE.MULT 関数

MODE.MULT 関数は、データセットの最頻値（最も頻繁に出現する値）を垂直配列として返します。

データに複数の最頻値がある場合に、それらすべてを配列で返すことができます。配列数式として入力する必要があります。

関数の構文

MODE.MULT(数値1, [数値2], …)

数値1, [数値2], …：最頻値を求めたい 1〜255 個の数値、または数値を含む配列やセル範囲を指定します。

関数の使用例

テストの点数データから、最頻値をすべて求めます。

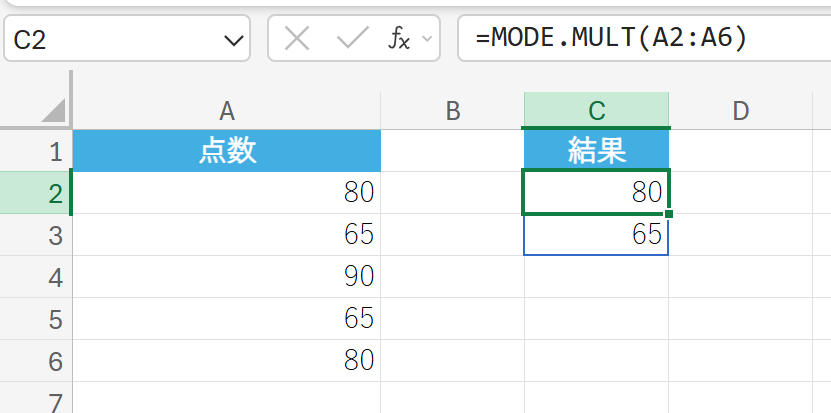
62. MODE.SNGL 関数

MODE.SNGL 関数は、データセットの最頻値（最も頻繁に出現する値）を 1 つだけ返します。

複数の最頻値がある場合は、最初に見つかった値を返します。以前の MODE 関数と同じ機能です。

関数の構文

MODE.SNGL(数値1, [数値2], …)

数値1, [数値2], …：最頻値を求めたい 1〜255 個の数値、または数値を含む配列やセル範囲を指定します。

関数の使用例

上記のデータから、最頻値を 1 つだけ求めます。

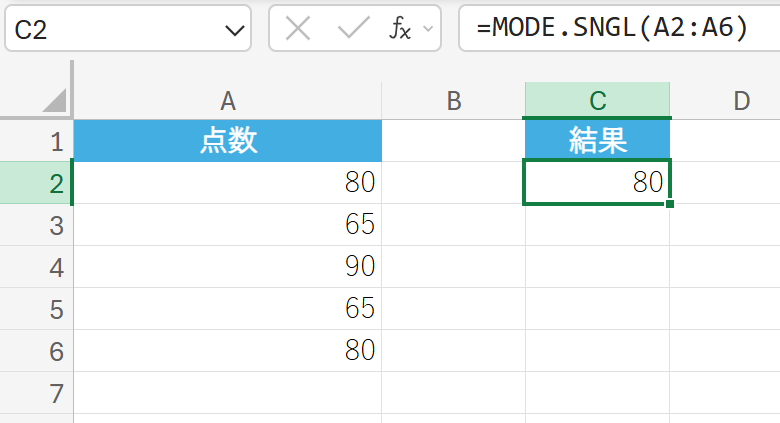
解説

最初に出現する最頻値 (80) が返されます。

63. NEGBINOM.DIST 関数

NEGBINOM.DIST 関数は、負の二項分布の確率を返します。

負の二項分布は、特定の回数 k の成功を得るまでに、何回 x の失敗が発生するかの確率を計算するために使われます（例：成功率 p の試行を繰り返し、3回目の成功を得るまでに 5 回失敗する確率）。

関数の構文

NEGBINOM.DIST(失敗数, 成功数, 成功率, 累積)

失敗数：失敗の回数 x を指定します。
成功数：しきい値となる成功の回数 k を指定します。
成功率：1 回の試行における成功の確率 p を指定します。
累積：論理値で、TRUE（累積確率）またはFALSE（単独の確率）を指定します。

関数の使用例

ある営業担当者が、新規顧客に電話をかけて契約を獲得する成功率（確率）は**20%** であるとします。

この担当者が、目標の 3 件の契約（成功数 r=3）を獲得するまでに、以下の失敗数となる確率を計算しなさい。

厳密に 5 回の失敗（k=5）が発生する確率。
5 回以下の失敗（k≤5）で目標達成となる確率。

64. NORM.DIST 関数

NORM.DIST 関数は、正規分布の累積分布関数または確率密度関数の値を返します。

正規分布は、自然界や社会現象における多くの事象をモデル化する、最も重要な連続確率分布です。

関数の構文

NORM.DIST(x, 平均, 標準偏差, 累積)

x：分布を評価する値を指定します。
平均：分布の算術平均を指定します。
標準偏差：分布の標準偏差を指定します。
累積：論理値で、TRUE（累積分布関数）またはFALSE（確率密度関数）を指定します。

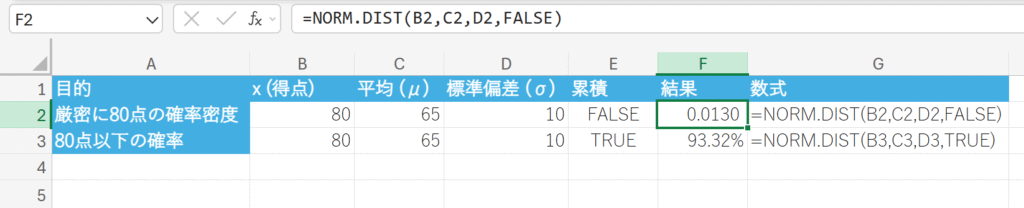
関数の使用例

あるクラスで行われたテストの得点が正規分布に従うと仮定します。テスト結果は以下の通りです。

平均 (μ)： 65 点
標準偏差 (σ)： 10 点

このとき、以下の確率を計算しなさい。
80 点以下の得点である確率（割合）
厳密に 80 点である確率密度

65. NORM.INV 関数

NORM.INV 関数は、正規分布の累積分布関数の逆関数値を返します。

確率が与えられたときに、その確率に対応する x の値を求めます。

関数の構文

NORM.INV(確率, 平均, 標準偏差)

確率：正規分布に関連付けられた累積確率を指定します (0～1)。
平均：分布の算術平均を指定します。
標準偏差：分布の標準偏差を指定します。

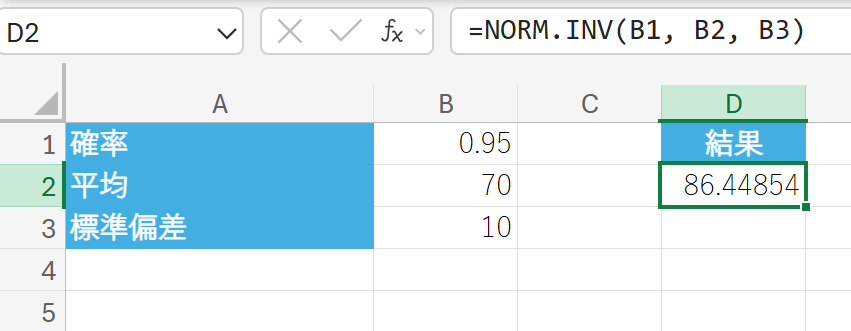
関数の使用例

平均 70、標準偏差 10 の正規分布において、累積確率が 95% となる x の値を求めます。

66. NORM.S.DIST 関数

NORM.S.DIST 関数は、標準正規分布の累積分布関数の値を返します。

標準正規分布（平均 μ=0、標準偏差 σ=1 の正規分布）を評価します。

関数の構文

NORM.S.DIST(Z, 累積)

Z：標準正規分布を評価する z 値を指定します。
累積：論理値で、TRUE（累積分布関数）またはFALSE（確率密度関数）を指定します。

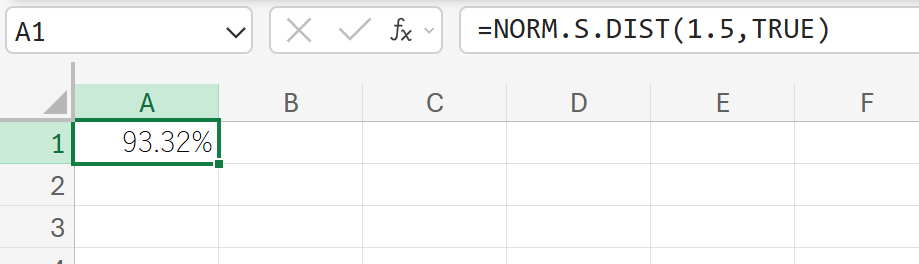
関数の使用例

z 値が 1.5 の場合の累積確率を求めます。

67. NORM.S.INV 関数

NORM.S.INV 関数は、標準正規分布の累積分布関数の逆関数値を返します。

確率が与えられたときに、その確率に対応する z 値を求めます。

関数の構文

NORM.S.INV(確率)

確率：標準正規分布に関連付けられた累積確率を指定します (0～1)。

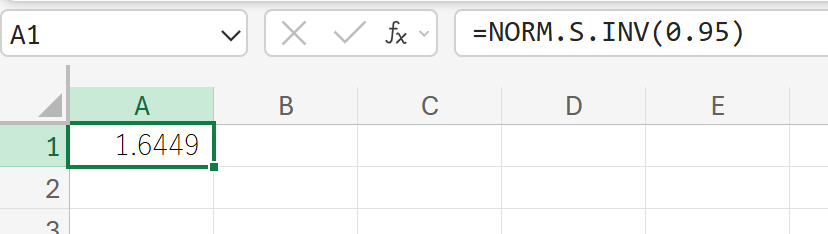
関数の使用例

標準正規分布において、累積確率が 95% となる z 値を求めます。

68. PERCENTILE.EXC 関数

PERCENTILE.EXC 関数は、0 と 1 を除く範囲の K 番目のパーセンタイル値を返します。

データセットの分布を知るために使われ、例えば、K=0.9 の場合、データの 90% がその値以下であることを意味します。0 と 1 を除くため、K は 0 より大きく 1 より小さくなければなりません。

関数の構文

PERCENTILE.EXC(配列, K)

配列：パーセンタイル値を求めるデータを含む配列またはセル範囲を指定します。
K： 0 から 1 までのパーセンタイル値を指定します。

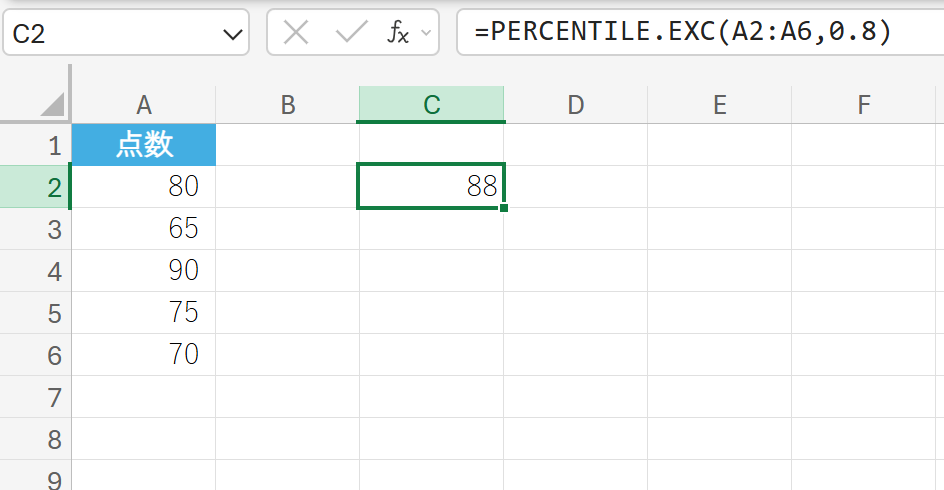
関数の使用例

テストの点数データの 80 パーセンタイル値を求めます。

69. PERCENTILE.INC 関数

PERCENTILE.INC 関数は、0 と 1 を含む範囲の K 番目のパーセンタイル値を返します。

PERCENTILE.EXC と異なり、K に 0 や 1 を指定できます。PERCENTILE 関数と同じ機能です。

関数の構文

PERCENTILE.INC(配列, K)

配列：パーセンタイル値を求めるデータを含む配列またはセル範囲を指定します。
K： 0 から 1 までのパーセンタイル値を指定します。

関数の使用例

テストの点数データの 90 パーセンタイル値を求めます。

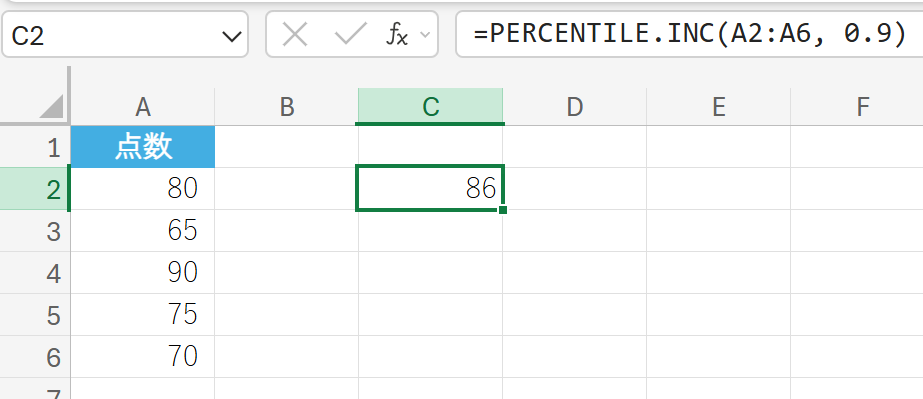
70. PERCENTRANK.EXC 関数

PERCENTRANK.EXC 関数は、0 と 1 を除く範囲で、データセットにおける特定の値の順位 (パーセンタイル) を返します。

特定のデータ値が、データセット全体の中でどの程度の割合で小さい方から数えて何番目に位置するかを示します。

関数の構文

PERCENTRANK.EXC(配列, x, [桁数])

配列：データセットを含む配列またはセル範囲を指定します。
x：順位を求める値を指定します。
[桁数]：戻り値の小数点以下の桁数を指定します（省略すると 3 桁）。

関数の使用例

テストの点数データにおいて、点数 75 が全体の何パーセンタイルに位置するかを求めます。

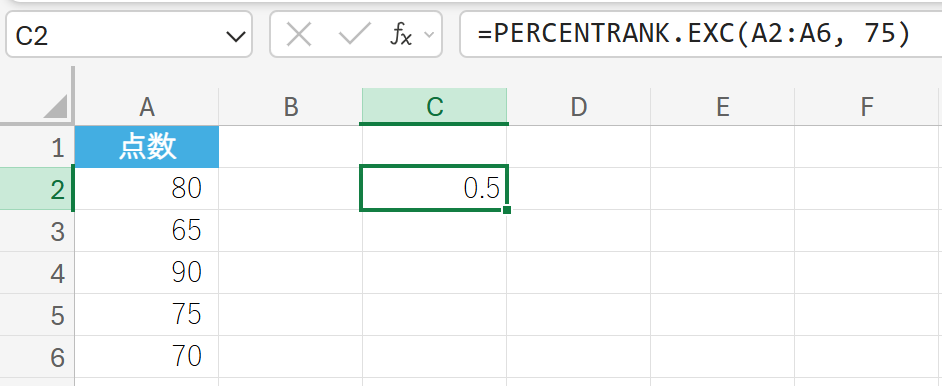
71. PERCENTRANK.INC 関数

PERCENTRANK.INC 関数は、0 と 1 を含む範囲で、データセットにおける特定の値の順位 (パーセンタイル) を返します。

PERCENTRANK.EXC と異なり、0 と 1 を含むため、計算方法が若干異なります。PERCENTRANK 関数と同じ機能です。

関数の構文

PERCENTRANK.INC(配列, x, [桁数])

配列：データセットを含む配列またはセル範囲を指定します。
x：順位を求める値を指定します。
[桁数]：戻り値の小数点以下の桁数を指定します（省略すると 3 桁）。

関数の使用例

テストの点数データにおいて、点数 75 が全体の何パーセンタイルに位置するかを求めます。

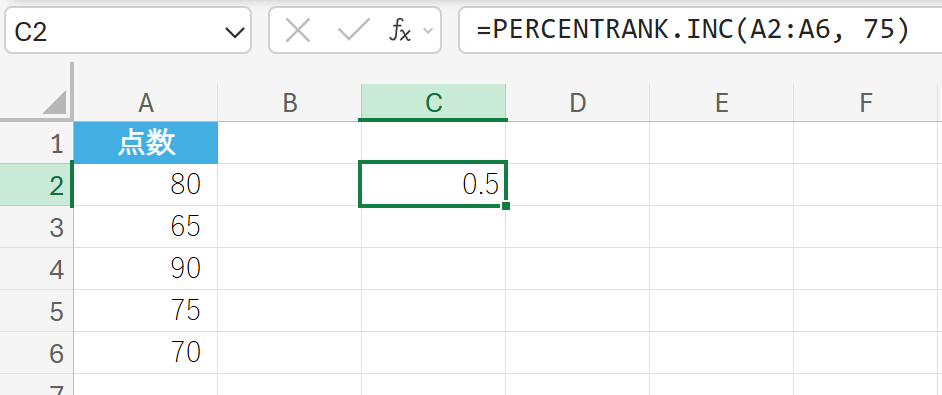
72. PERMUT 関数

PERMUT 関数は、指定された総数から特定の個数を選択する順列の数を返します。

順序が重要である場合の組み合わせの数を計算します（例：5 枚のカードから 3 枚を選んで並べる順序の数）。

関数の構文

PERMUT(総数, 抜き取り数)

総数：項目の総数（母集団）を指定します。
抜き取り数：総数から抜き取る項目の数を指定します。

関数の使用例

10 人の中から、議長、副議長、書記の 3 つの役職を選出する場合の順列の数を求めます。

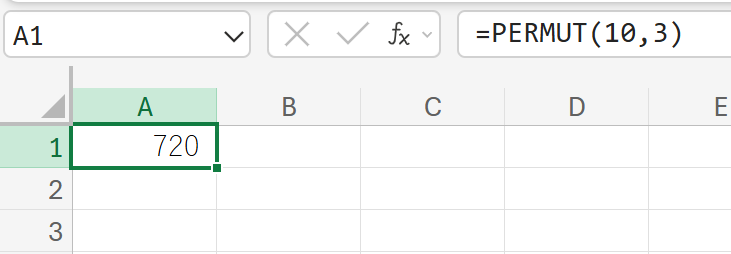
73. PERMUTATIONA 関数

PERMUTATIONA 関数は、重複を許す順列の数を返します。

抜き取った項目を元に戻し、同じ項目を再び抜き取ることが可能である場合の組み合わせの数を計算します（例：3 桁の暗証番号を作る場合の順列の数。000～999 の 10 個の数字から 3 回選ぶ）。

関数の構文

PERMUTATIONA(総数, 抜き取り数)

総数：項目の総数（母集団）を指定します。
抜き取り数：順列に含まれる項目の数を指定します。

関数の使用例

10 種類の数字から 3 桁のパスワードを作る場合の順列の数を求めます。

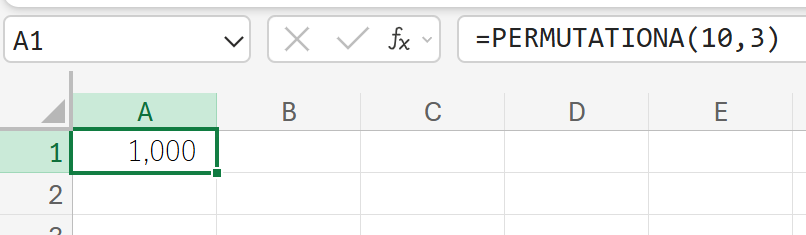
74. PHI 関数

PHI 関数は、標準正規分布の確率密度関数の値を返します。

NORM.S.DIST(Z, FALSE) と同じ結果を返しますが、より簡潔な関数名で提供されています。

関数の構文

PHI(Z)

Z：標準正規分布を評価する z 値を指定します。

関数の使用例

z 値が 1.5 の場合の確率密度関数の値を求めます。

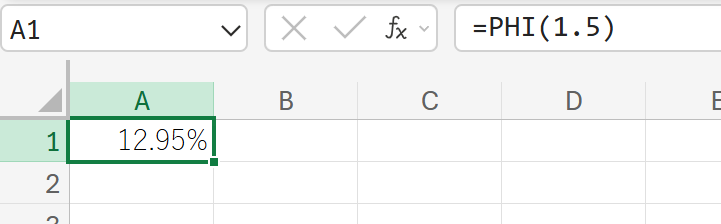
75. POISSON.DIST 関数

POISSON.DIST 関数は、ポアソン分布の確率を返します。

ポアソン分布は、特定の時間間隔や空間内でまれな事象が何回発生するかの確率を計算するために使われます（例：1 時間あたりにかかってくる電話の回数や、1 ページあたりの誤植の数）。

関数の構文

POISSON.DIST(x, 平均, 累積)

x：事象の発生回数を指定します。
平均：期待される平均発生回数 λ を指定します。
累積：論理値で、TRUE（累積確率）またはFALSE（単独の確率）を指定します。

関数の使用例

平均して 3 回の事象が発生する場合に、ちょうど 4 回の事象が発生する単独の確率を求めます。

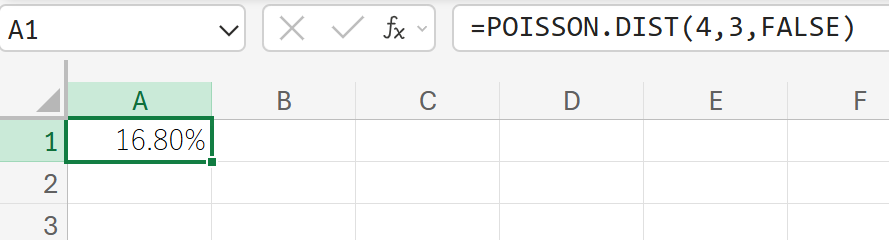
76. PROB 関数

PROB 関数は、特定の範囲内の値に対する確率を返します。

確率変数とそれに対応する確率が与えられたときに、指定された範囲に含まれる確率を求めます。

関数の構文

PROB(確率変数, 確率, 下限, [上限])

確率変数：確率変数 (数値) を含む配列またはセル範囲を指定します。
確率：それぞれの確率変数に対応する確率を含む配列またはセル範囲を指定します。
下限：確率を計算する範囲の下限を指定します。
[上限]：確率を計算する範囲の上限を指定します。省略すると、下限の確率変数の単独の確率を返します。

関数の使用例

通常の6面サイコロを1回振るときの目の確率を分析します。目が 3 以上 5 以下である確率は？

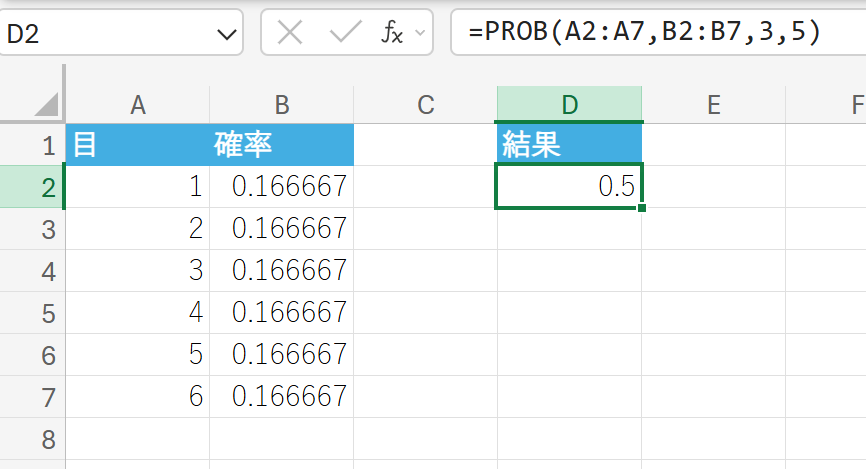
77. QUARTILE.EXC 関数

QUARTILE.EXC 関数は、0 と 4 を除く範囲で、データセットの四分位数を返します。

四分位数は、データを 4 等分する 3 つの値で、データの散らばり具合を分析するのに使われます。

関数の構文

QUARTILE.EXC(配列, 四分位)

配列：四分位数を求めるデータを含む配列またはセル範囲を指定します。
四分位：返す四分位数を指定します（1、2、3 のいずれか）。

四分位	意味
1	第 1 四分位数 (Q1、25 パーセンタイル)
2	第 2 四分位数 (Q2、中央値)
3	第 3 四分位数 (Q3、75 パーセンタイル)

関数の使用例

テストの点数データの第 1 四分位数 (Q1) を求めます。

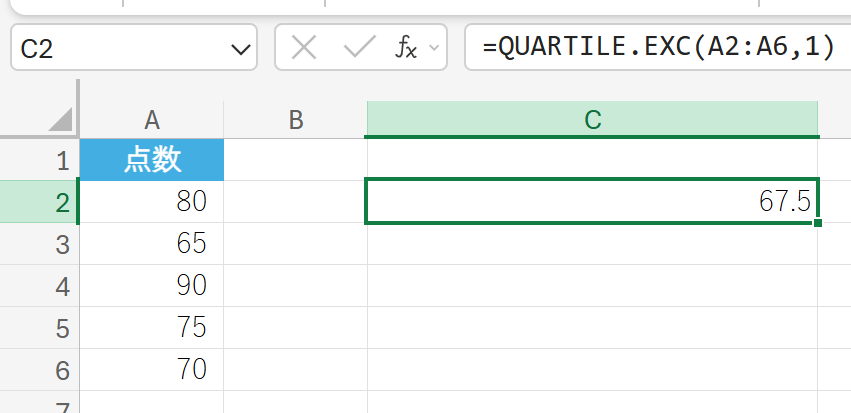
78. QUARTILE.INC 関数

QUARTILE.INC 関数は、0 と 4 を含む範囲で、データセットの四分位数を返します。

QUARTILE.EXC と異なり、0 (最小値) や 4 (最大値) も指定できます。QUARTILE 関数と同じ機能です。

関数の構文

QUARTILE.INC(配列, 四分位)

配列：四分位数を求めるデータを含む配列またはセル範囲を指定します。
四分位：返す四分位数を指定します（0、1、2、3、4 のいずれか）。

関数の使用例

テストの点数データの第 1 四分位数 (Q1) を求めます。

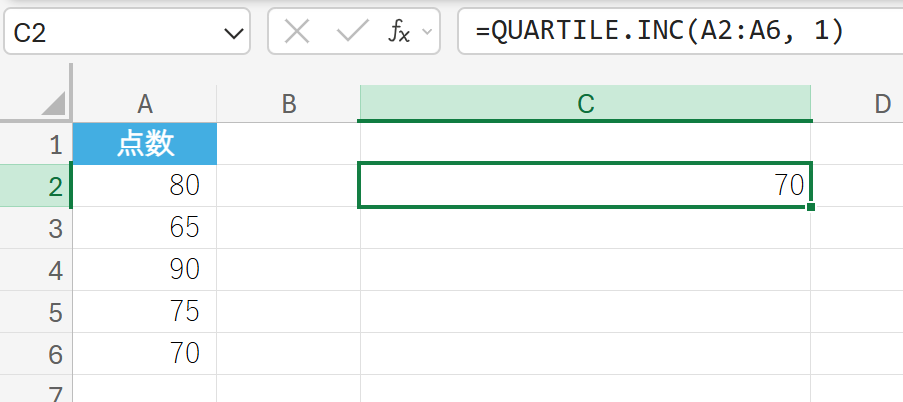
79. RANK.AVG 関数

RANK.AVG 関数は、数値の順位（ランク）を返します。

同じ値を持つ数値がある場合、その順位の平均値を返します（例：同じく 3 位と 4 位の 2 つの値があった場合、両方に 3.5 を返します）。

関数の構文

RANK.AVG(数値, 参照, [順序])

数値：順位を調べる数値を指定します。
参照：数値を含む配列またはセル範囲を指定します。
[順序]：順位の付け方を指定します。0 (または省略) は降順、1 は昇順です。

関数の使用例

テストの点数データにおいて、点数 75 の順位を降順で求めます。

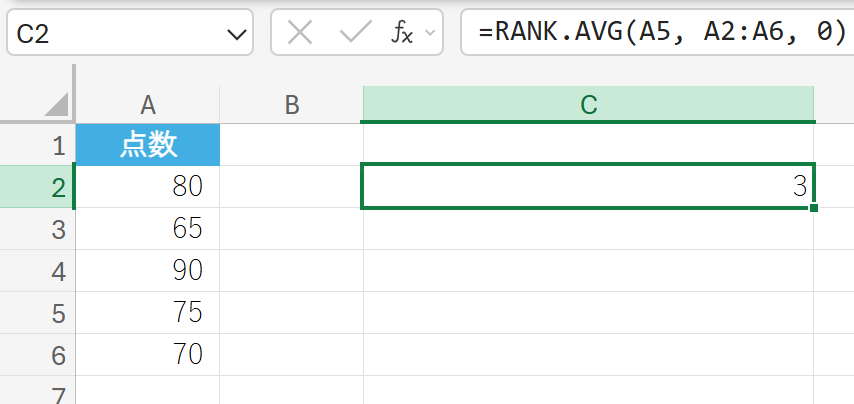
80. RANK.EQ 関数

RANK.EQ 関数は、数値の順位（ランク）を返します。

同じ値を持つ数値がある場合、最も上位の順位を返します（例：同じく 3 位と 4 位の 2 つの値があった場合、両方に 3 を返します）。RANK 関数と同じ機能です。

関数の構文

RANK.EQ(数値, 参照, [順序])

数値：順位を調べる数値を指定します。
参照：数値を含む配列またはセル範囲を指定します。
[順序]：順位の付け方を指定します。0 (または省略) は降順、1 は昇順です。

関数の使用例

上記のデータで、点数 75 の順位を求めます。

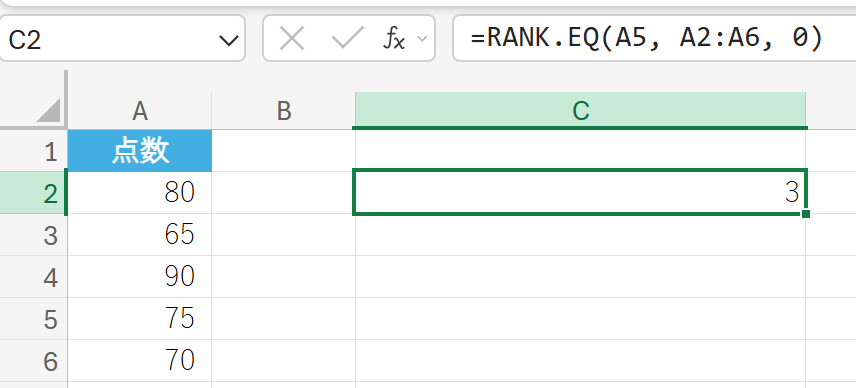
81. RSQ 関数

RSQ 関数は、相関係数の 2 乗 (決定係数 R2) を返します。

決定係数 R2 は、線形回帰において、独立変数 (x) が従属変数 (y) の変動をどれだけ説明できるかを示す指標です。0 から 1 の値を取り、1 に近いほど回帰モデルの当てはまりが良いことを示します。

関数の構文

RSQ(既知の y, 既知の x)

既知の y, 既知の x：既知のデータセット（従属変数と独立変数）を指定します。

関数の使用例

ある企業の過去5か月間の広告費と売上のデータを表に示しました。このデータを用いて、広告費（x）が売上（y）の変動をどの程度説明できるか、決定係数 (R2) を計算しなさい。

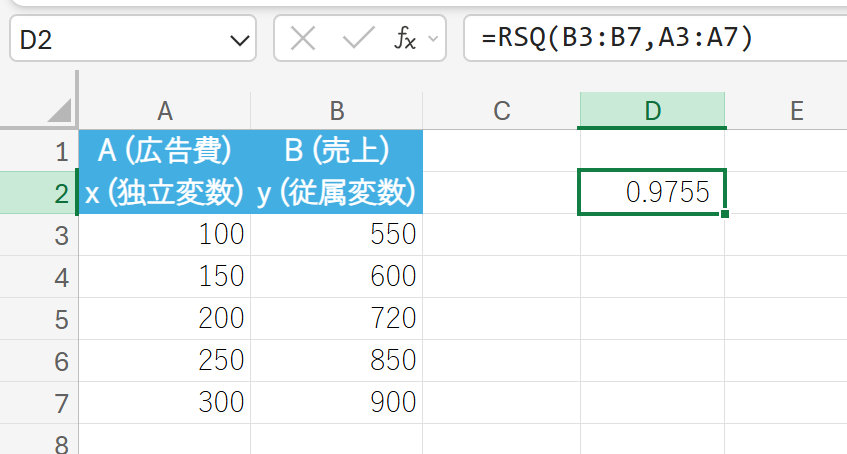
この結果は、「売上（y）の変動の約 98.5% が、広告費（x）の変動によって説明される」ことを示しており、広告費と売上の間には非常に強い線形的な関係があり、回帰モデルの適合度が高いと判断できます。

82. SKEW 関数

SKEW 関数は、データセットの歪度 (わいど) を返します。

歪度は、データの分布が左右対称であるかどうかを示す指標です。正の値は右側に裾を引く（右に歪んだ）分布、負の値は左側に裾を引く（左に歪んだ）分布であることを示します。正規分布の歪度は 0 です。

関数の構文

SKEW(数値1, [数値2], …)

数値1, [数値2], …：歪度を計算したい 1〜255 個の数値、または数値を含む配列やセル範囲を指定します。

関数の使用例

あるテストの点数データの歪度を求め、分布の偏りを調べます。

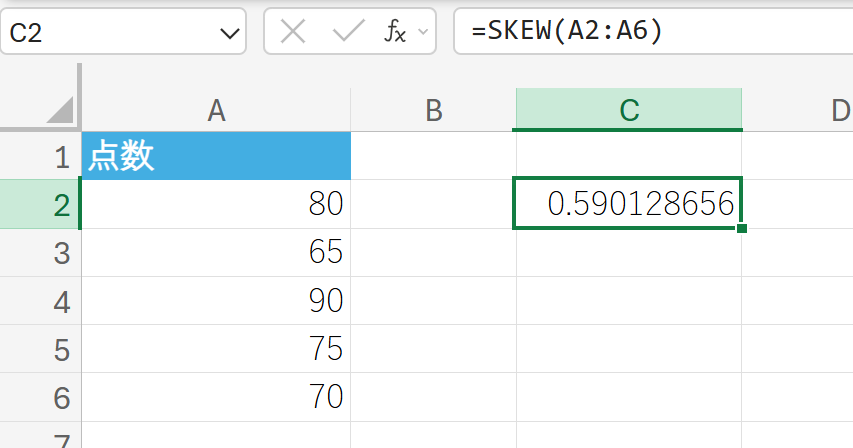
解説

正の値なので、分布の裾が右側に長く伸びている（高得点側に外れ値がある）傾向があることを示します。

83. SKEW.P 関数

SKEW.P 関数は、母集団の歪度を返します。

SKEW 関数は標本の歪度を返しますが、SKEW.P 関数はデータが母集団全体であると仮定して歪度を計算します。標本サイズが小さい場合、SKEW.P の方が SKEW よりも絶対値が小さくなる傾向があります。

関数の構文

SKEW.P(数値1, [数値2], …)

数値1, [数値2], …：歪度を計算したい 1〜255 個の数値、または数値を含む配列やセル範囲を指定します。

関数の使用例

上記のデータ（これを母集団全体と仮定）の歪度を求めます。

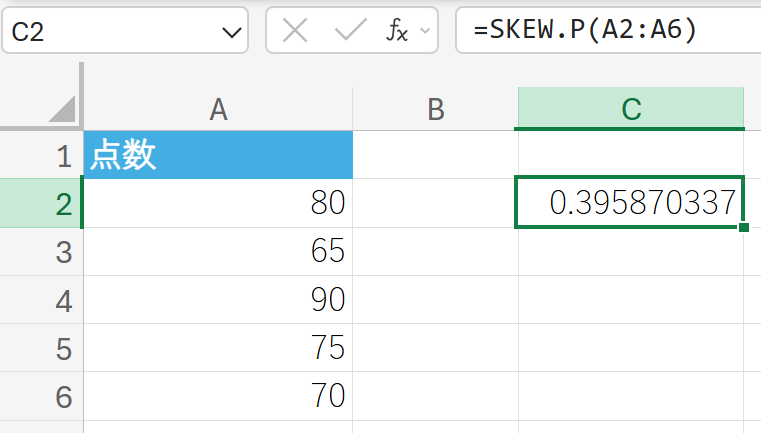
84. SLOPE 関数

SLOPE 関数は、線形回帰直線の傾きを計算します。

線形回帰直線 y=ax+b における、x の変化に対する y の変化率（傾き a）を計算します。

関数の構文

SLOPE(既知の y, 既知の x)

既知の y, 既知の x：既知のデータセット（従属変数と独立変数）を指定します。

関数の使用例

広告費 (x) と売上 (y) のデータに基づき、回帰直線の傾きを求めます。

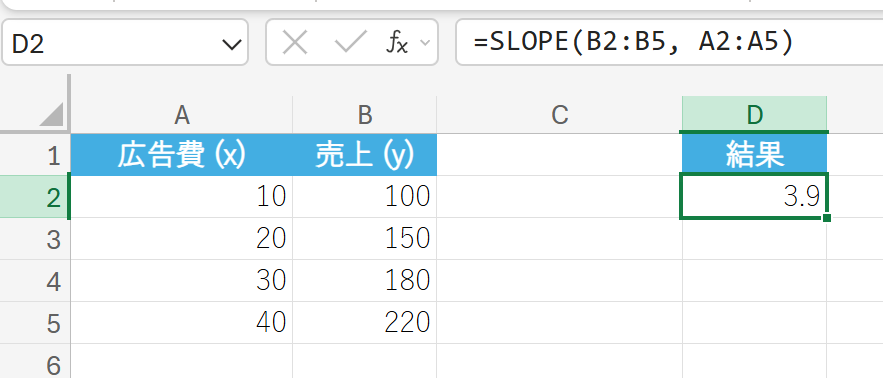
解説

広告費が10万円増えるごとに、売上は平均39万円増加すると予測されます。

85. SMALL 関数

SMALL 関数は、データセット内の K 番目に小さな値を返します。

最小値 (1 番目に小さな値) や 2 番目に小さな値などを簡単に求めたいときに使います。LARGE 関数と対になります。

関数の構文

SMALL(配列, K)

配列：K 番目に小さな値を求めるデータを含む配列またはセル範囲を指定します。
K：返す順位を指定します (1 は最小値、2 は 2 番目に小さな値)。

関数の使用例

テストの点数データから、2 番目に小さな値（下から 2 番目の点数）を求めます。

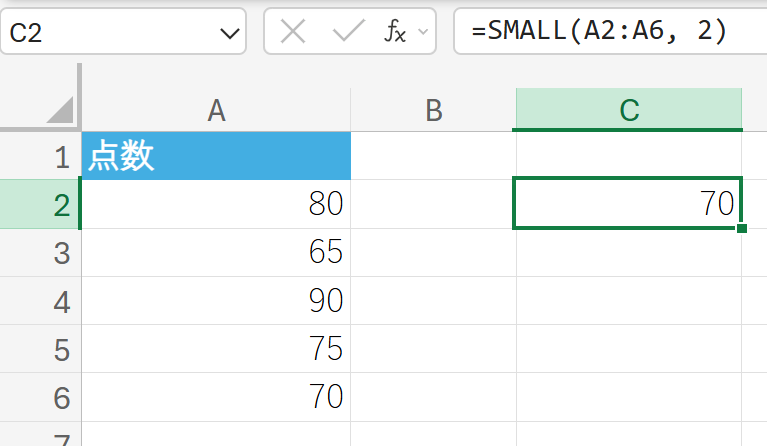
86. STANDARDIZE 関数

STANDARDIZE 関数は、指定された平均と標準偏差を持つ分布から、Z 値（標準化された値）を返します。

データ値を、平均 μ=0、標準偏差 σ=1 の標準正規分布における値に変換するために使用されます。

Z=σx−μ

関数の構文

STANDARDIZE(x, 平均, 標準偏差)

x：標準化する値を指定します。
平均：分布の算術平均を指定します。
標準偏差：分布の標準偏差を指定します。

関数の使用例

平均 70、標準偏差 10 のテストで、点数 80 を標準化します。

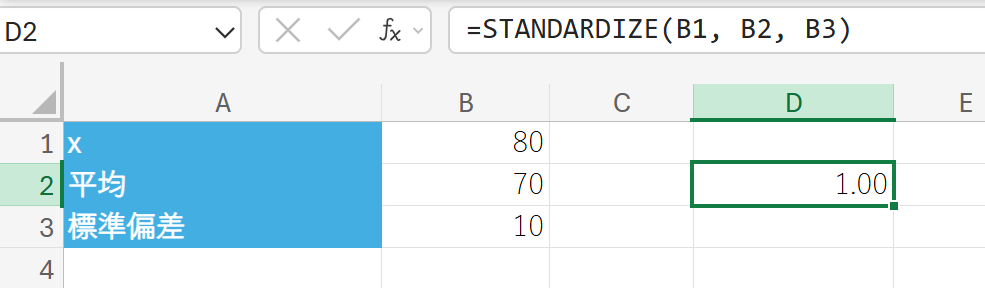
87. STDEV.P 関数

STDEV.P 関数は、母集団の標準偏差を返します。

データが母集団全体であると仮定して標準偏差を計算します。標準偏差は、データが平均値の周りにどれだけ散らばっているかを示す最も一般的な指標です。

関数の構文

STDEV.P(数値1, [数値2], …)

数値1, [数値2], …：標準偏差を計算したい 1〜255 個の数値、または数値を含む配列やセル範囲を指定します。

関数の使用例

テストの点数データ（これを母集団全体と仮定）の標準偏差を求めます。

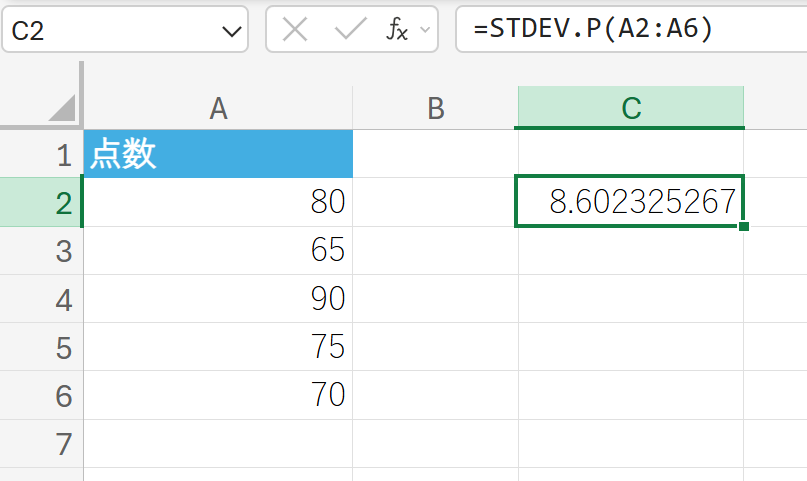
88. STDEV.S 関数

STDEV.S 関数は、標本の標準偏差を返します。

データが母集団の標本であると仮定して標準偏差を計算します。一般的に、手元のデータが母集団の一部である場合、こちらを使用します。STDEV 関数と同じ機能です。

関数の構文

STDEV.S(数値1, [数値2], …)

数値1, [数値2], …：標準偏差を計算したい 1〜255 個の数値、または数値を含む配列やセル範囲を指定します。

関数の使用例

テストの点数データ（これを標本と仮定）の標準偏差を求めます。

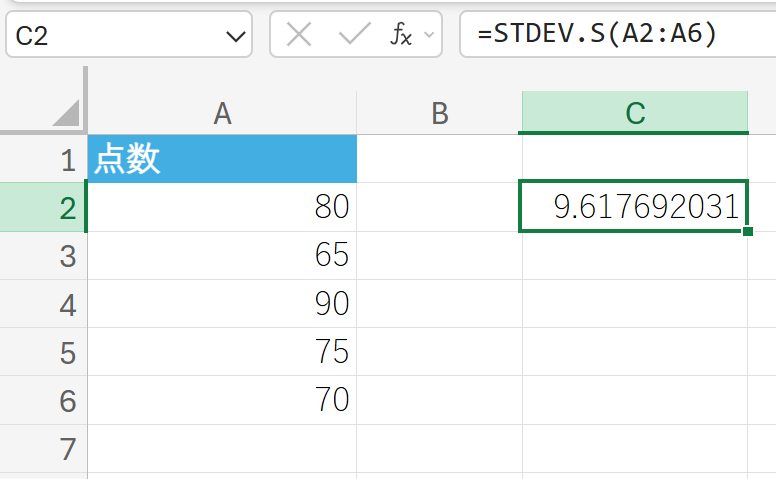
89. STDEVA 関数

STDEVA 関数は、標本の標準偏差を返しますが、論理値や文字列も評価の対象とします。

引数に含まれる文字列を 0、TRUEを 1、FALSEを 0 として計算の対象に含めます。

関数の構文

STDEVA(値1, [値2], …)

値1, [値2], …：標準偏差を計算したい 1〜255 個の引数、または配列やセル範囲を指定します。

関数の使用例

テストの点数データに論理値や文字列を含めて標準偏差を求めます。

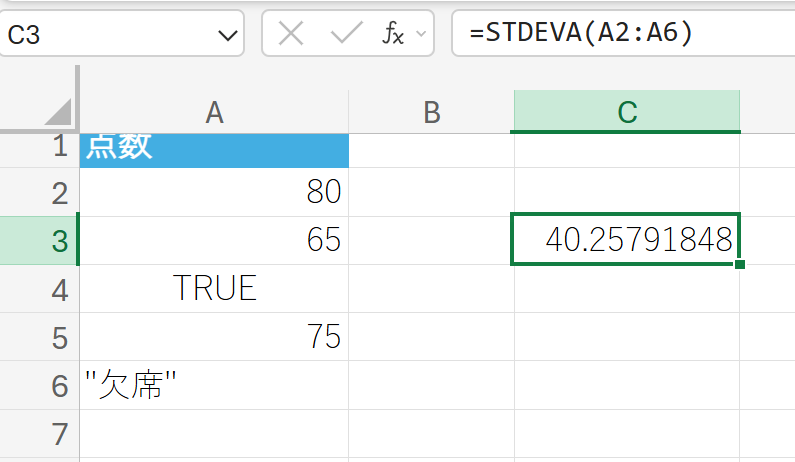
90. STDEVPA 関数

STDEVPA 関数は、母集団の標準偏差を返しますが、論理値や文字列も評価の対象とします。

引数に含まれる文字列を 0、TRUEを 1、FALSEを 0 として計算の対象に含めます。

関数の構文

STDEVPA(値1, [値2], …)

値1, [値2], …：標準偏差を計算したい 1〜255 個の引数、または配列やセル範囲を指定します。

関数の使用例

上記のデータ（これを母集団全体と仮定）の標準偏差を求めます。

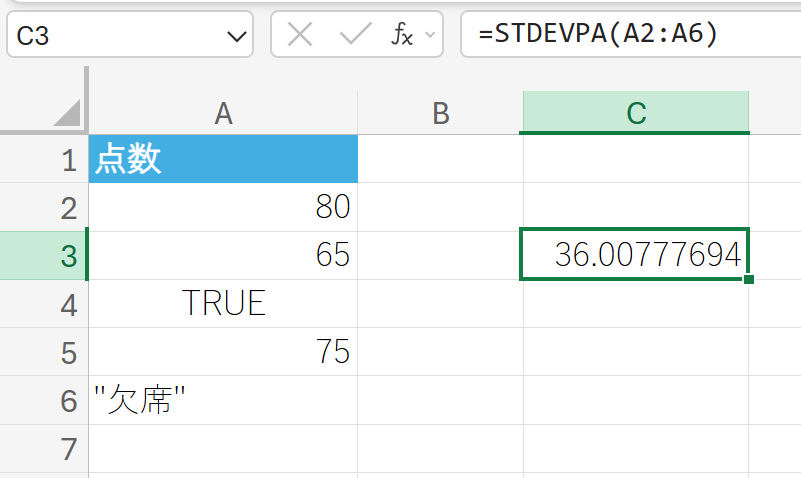
91. STEYX 関数

STEYX 関数は、回帰分析における y の予測標準誤差を返します。

この値は、回帰直線上の y 予測値から、観測された y 値がどれだけ平均的に離れているか（予測の精度）を示します。値が小さいほど、回帰モデルの予測精度が高いことを意味します。

関数の構文

STEYX(既知の y, 既知の x)

既知の y, 既知の x：既知のデータセット（従属変数と独立変数）を指定します。

関数の使用例

広告費と売上のデータに基づき、売上予測の標準誤差を求めます。

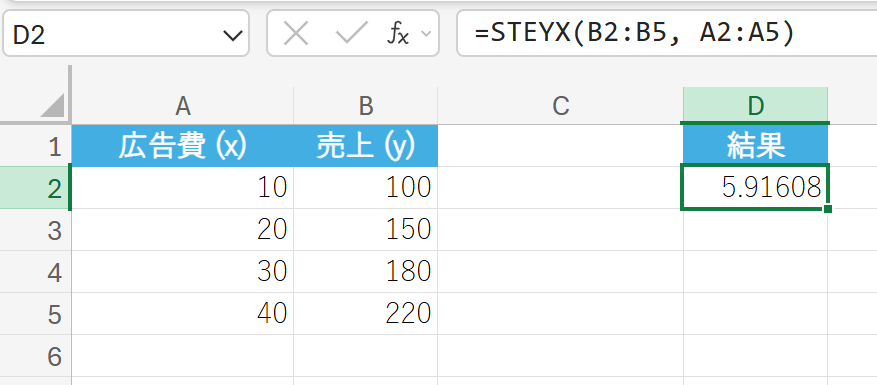
解説

予測される売上と実際の売上との差は、平均して約5.91万円であることを示します。

92. T.DIST 関数

T.DIST 関数は、スチューデントの t 分布の値を返します。

t 分布は、母集団の標準偏差が未知の場合や、標本サイズが小さい場合に、平均値の検定（t 検定）に使用されます。

関数の構文

T.DIST(x, 自由度, 累積)

x：分布を評価する t 値を指定します。
自由度：分布の自由度を指定します。
累積：論理値で、TRUE（累積分布関数）またはFALSE（確率密度関数）を指定します。

関数の使用例

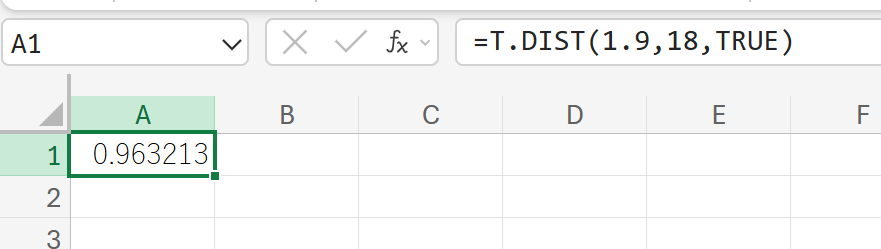
ある統計データ分析で、t統計量（t値）が1.9と計算されその検定に使われたデータの自由度が18 であったとします。

t値 (x)： 1.9
自由度： 18

このt値1.9の累積確率（1.9以下の確率）を計算しなさい。

93. T.DIST.2T 関数

T.DIST.2T 関数は、スチューデントの t 分布の両側確率を返します。

t 検定の両側検定における P 値を計算する際に使われます。

関数の構文

T.DIST.2T(x, 自由度)

x：分布を評価する t 値 (絶対値) を指定します。
自由度：分布の自由度を指定します。

関数の使用例

自由度 10 の t 分布において、t 値が 2.0 以上の絶対値を持つ確率（両側確率）を求めます。

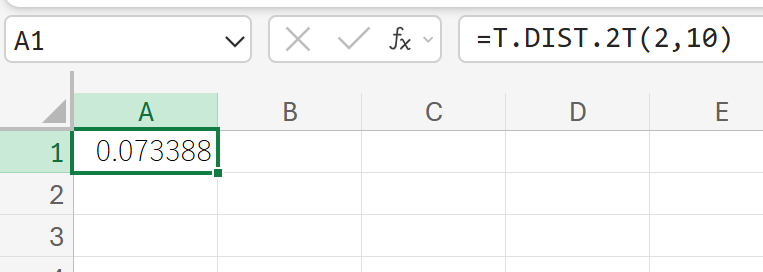
94. T.DIST.RT 関数

T.DIST.RT 関数は、スチューデントの t 分布の右側確率を返します。

t 検定の片側検定における P 値を計算する際に使われます。

関数の構文

T.DIST.RT(x, 自由度)

x：分布を評価する t 値を指定します。
自由度：分布の自由度を指定します。

関数の使用例

自由度 10 の t 分布において、t 値が 2.0 以上の確率（右側確率）を求めます。

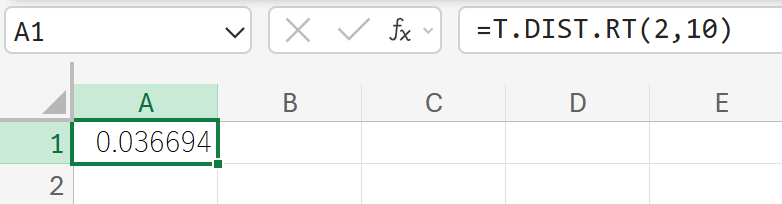
95. T.INV 関数

T.INV 関数は、スチューデントの t 分布の累積分布関数の逆関数値を返します。

与えられた累積確率に対応する t 値を求めます。

関数の構文

T.INV(確率, 自由度)

確率：t 分布に関連付けられた累積確率を指定します (0～1)。
自由度：分布の自由度を指定します。

関数の使用例

自由度 10 の t 分布において、累積確率が 95% となる t 値を求めます。

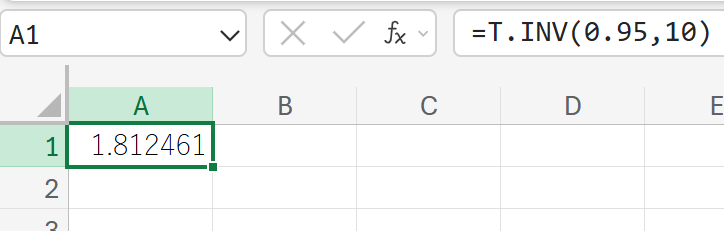
96. T.INV.2T 関数

T.INV.2T 関数は、スチューデントの t 分布の両側確率の逆関数値を返します。

両側検定における棄却域の境界（クリティカル値）を計算するために使われます。

関数の構文

T.INV.2T(確率, 自由度)

確率：t 分布に関連付けられた両側確率（有意水準 α）を指定します (0～1)。
自由度：分布の自由度を指定します。

関数の使用例

自由度 10 の t 分布において、両側確率が 5% (α=0.05) となる t 値を求めます。

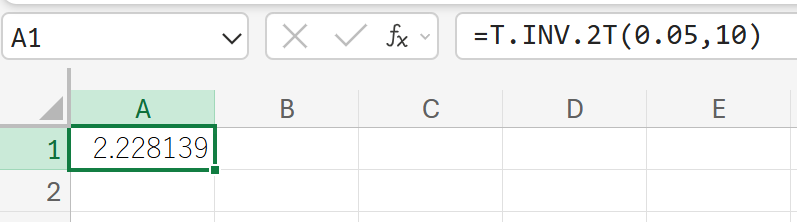
97. T.TEST 関数

T.TEST 関数は、t 検定の結果（P 値）を返します。

2つの標本の平均に統計的に有意な差があるかどうかを検定するために使われます。

関数の構文

T.TEST(配列1, 配列2, 尾部, 種類)

配列1, 配列2：検定するデータセットを指定します。
尾部：検定の種類（片側 1 または両側 2）を指定します。
種類：検定の形式（対応のある 1、等分散を仮定した 2、不等分散を仮定した 3）を指定します。

関数の使用例

2つのグループのテストの点数データ（分散は等しいと仮定）の平均に差があるか、両側検定で調べます。

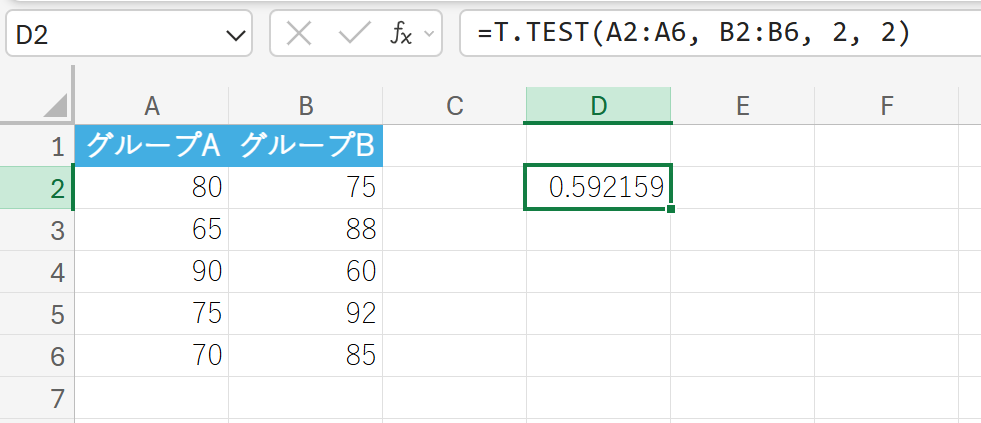
解説

この値が有意水準 (0.05) より大きいため、平均に有意な差があるとは言えません。

98. TRIMMEAN 関数

TRIMMEAN 関数は、データセットの P パーセントを除外した平均（刈り込み平均）を返します。

データセットの両端（最大値と最小値）から極端な外れ値を一定割合 P だけ除外した上で平均を計算するため、外れ値の影響を受けにくい代表値を求めるときに使われます。

関数の構文

TRIMMEAN(配列, 除去率)

配列：平均を求めるデータを含む配列またはセル範囲を指定します。
除去率：計算から除外するデータポイントの割合を 0 から 1 までのパーセント（または小数の比率）で指定します。

関数の使用例

テストの点数データの上位と下位からそれぞれ 20% (合計 40%) のデータを除外した平均を求めます。

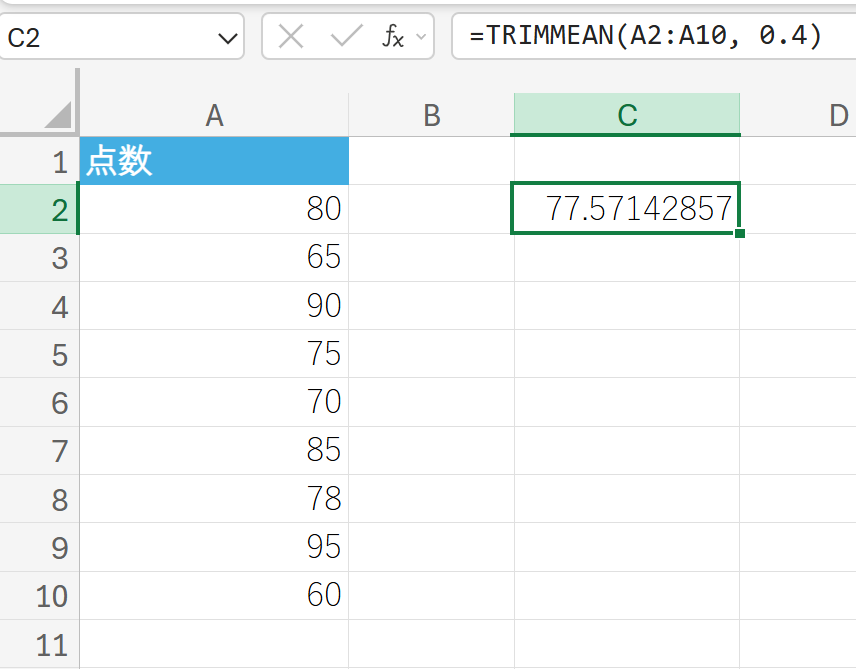
99. VAR.P 関数

VAR.P 関数は、母集団の分散を返します。

データが母集団全体であると仮定して分散を計算します。分散は、データの平均からの散らばり具合を数値化したもので、標準偏差の 2 乗に等しいです。

関数の構文

VAR.P(数値1, [数値2], …)

数値1, [数値2], …：分散を計算したい 1〜255 個の数値、または数値を含む配列やセル範囲を指定します。

関数の使用例

テストの点数データ（これを母集団全体と仮定）の分散を求めます。

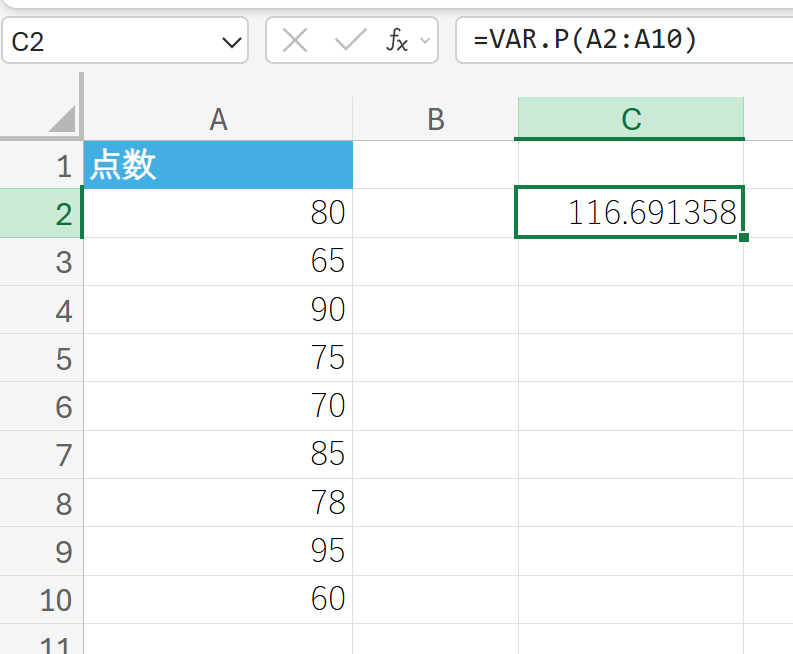
100. VAR.S 関数

VAR.S 関数は、標本の分散を返します。

データが母集団の標本であると仮定して分散を計算します。一般的に、手元のデータが母集団の一部である場合、こちらを使用します。VAR 関数と同じ機能です。

関数の構文

VAR.S(数値1, [数値2], …)

数値1, [数値2], …：分散を計算したい 1〜255 個の数値、または数値を含む配列やセル範囲を指定します。

関数の使用例

テストの点数データ（これを標本と仮定）の分散を求めます。

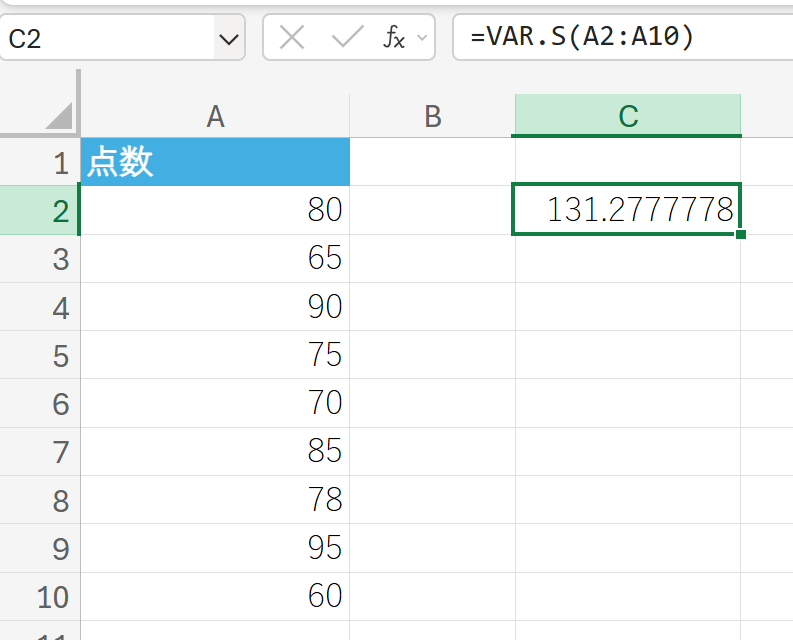
101. VARA 関数

VARA 関数は、標本の分散を返しますが、論理値や文字列も評価の対象とします。

引数に含まれる文字列を 0、TRUEを 1、FALSEを 0 として計算の対象に含めます。

関数の構文

VARA(値1, [値2], …)

値1, [値2], …：分散を計算したい 1〜255 個の引数、または配列やセル範囲を指定します。

関数の使用例

テストの点数データに論理値や文字列を含めて標本の分散を求めます。

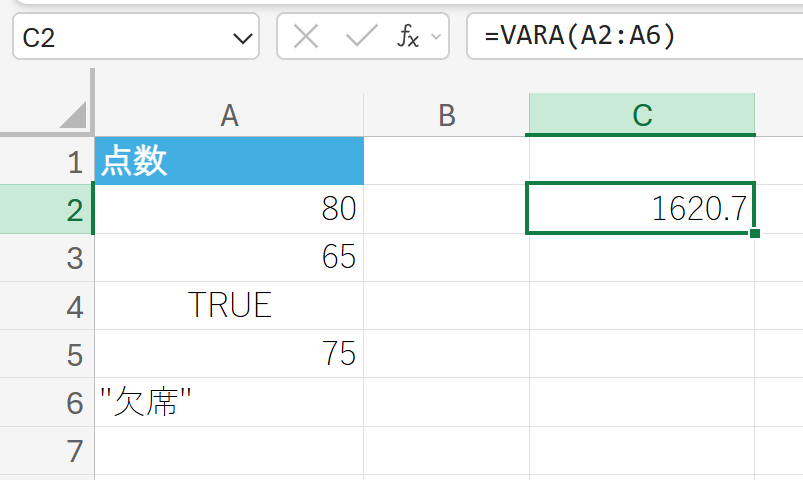
102. VARPA 関数

VARPA 関数は、母集団の分散を返しますが、論理値や文字列も評価の対象とします。

引数に含まれる文字列を 0、TRUEを 1、FALSEを 0 として計算の対象に含めます。

関数の構文

VARPA(値1, [値2], …)

値1, [値2], …：分散を計算したい 1〜255 個の引数、または配列やセル範囲を指定します。

関数の使用例

上記のデータ（これを母集団全体と仮定）の分散を求めます。

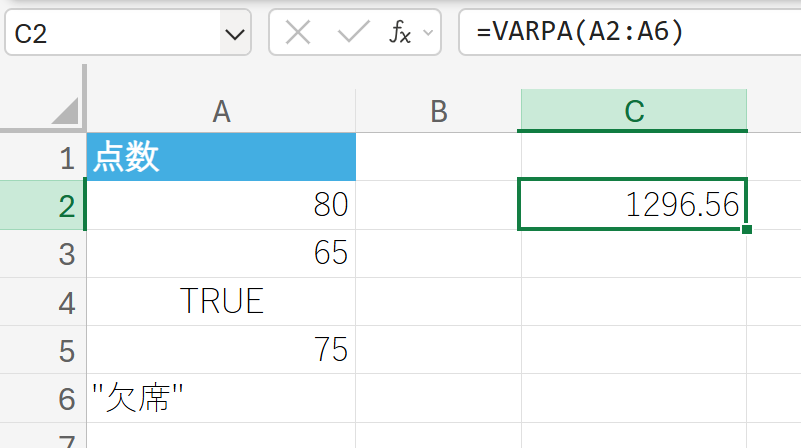
103. WEIBULL.DIST 関数

WEIBULL.DIST 関数は、ワイブル分布の累積分布関数または確率密度関数の値を返します。

ワイブル分布は、信頼性工学において、機器の故障時間など、寿命データをモデル化するために広く使われる分布です。

関数の構文

WEIBULL.DIST(x, α, β, 累積)

x：分布を評価する値を指定します。
α (アルファ)：形状パラメーターを指定します。
β (ベータ)：尺度パラメーターを指定します。
累積：論理値で、TRUE（累積分布関数）またはFALSE（確率密度関数）を指定します。

関数の使用例

ある電子部品の寿命が、以下のパラメーターを持つワイブル分布に従うと仮定します。

形状パラメーター (α)： 1.5 （α>1 のため、時間経過とともに故障率が増加する摩耗型）
尺度パラメーター (β)： 1000 時間

このとき、以下の確率を計算しなさい。
800 時間以下で故障する確率（つまり、800時間稼働後の累積故障確率）
厳密に 800 時間で故障する確率密度

104. Z.TEST 関数

Z.TEST 関数は、片側 Z 検定の P 値を返します。

母集団の標準偏差が既知である場合に、標本平均と想定される母平均との間に有意な差があるかどうかを検定するために使われます。

関数の構文

Z.TEST(配列, μ0, [σ])

配列：検定するデータセットを指定します。
μ0：母集団の平均の想定値（帰無仮説の平均）を指定します。
[σ]：母集団の標準偏差を指定します。省略すると、標本の標準偏差が使われます。

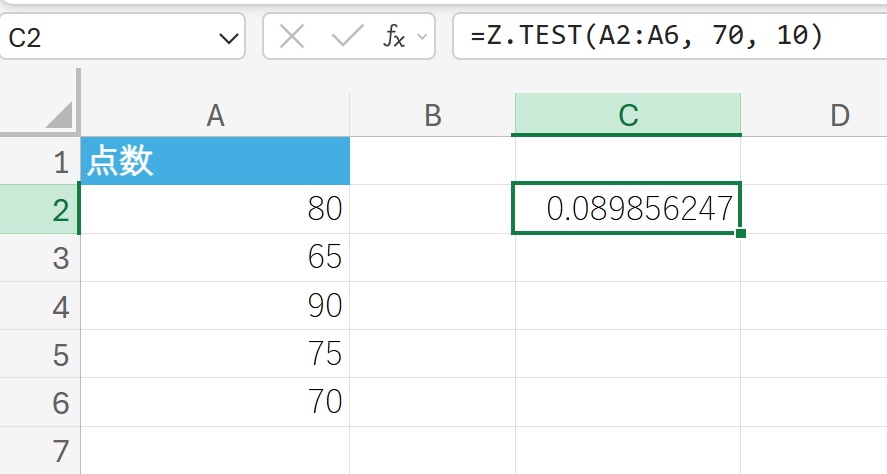
関数の使用例

ある母集団の平均が 70 であるという仮説 (μ0=70) を、標本データを用いて検定します。母標準偏差は既知で 10 とします。

記事のまとめと結びの言葉

Excel統計関数 104 種類の総まとめ

本記事では、Excelに用意されている 104 種類の統計関数を網羅的に解説し、それぞれの構文と実用的な使用例をご紹介しました。

統計関数は、データを集計する COUNT や SUM といった基本機能から、データが正規分布に従う確率を計算する NORM.DIST、仮説の真偽を検証する T.TEST や Z.TEST といった高度な検定まで、多岐にわたります。

主要な関数のカテゴリと用途

カテゴリ	主な用途	代表的な関数
基本統計量	データの中心と散らばりの把握	AVERAGE、MEDIAN、STDEV.S、VAR.S
条件付き集計	特定の条件を満たすデータの集計	COUNTIFS、SUMIFS、AVERAGEIFS、MAXIFS
順序・順位	データの大小関係や位置の把握	LARGE、SMALL、PERCENTILE、RANK
回帰分析・予測	データの傾向分析と将来予測	SLOPE、INTERCEPT、FORECAST、CORREL
確率分布	確率の計算とモデル化	NORM.DIST、BINOM.DIST、POISSON.DIST
統計的検定	仮説の検証と有意性の判断	T.TEST、Z.TEST、F.TEST、CHISQ.TEST