- Excelで三角関数を扱うときの最も重要なルール
- COS90°が0にならない本当の理由
- RADIANS関数やPI()関数の使い方
- Excelでの三角関数の基本的な計算方法（実用例付き）
- 角度を求める逆三角関数の使い方
- 計算時に役立つ注意点とエラーの対処法
そもそも三角関数って何？
直角三角形における辺の長さの比率（三角比）から発展し、角度を引数とする関数
Excelでは、主に以下の3つの関数を使います。
- SIN（サイン）：対辺÷斜辺の比率を求めます。
- COS（コサイン）：底辺÷斜辺の比率を求めます。
- TAN（タンジェント）：対辺÷底辺の比率を求めます。
これらの関数を使うことで、建物の高さを測ったり、物理学の計算をしたりと、様々な場面で活用できます。
なぜCOS90°は0にならない？Excelの「ラジアン」の秘密
「COS90°は0になるはずなのに、Excelで=COS(90)と計算したら、なぜか約-0.448…という変な値が出てきた…」
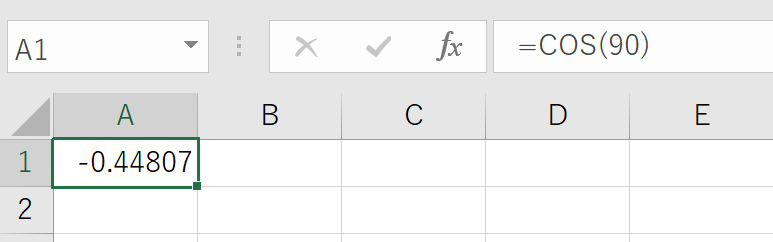
この現象は、Excelの三角関数が、私たちが普段使う「度（°）」ではなく、「ラジアン」という単位で計算しているからです。
度とラジアン、その根本的な違い
度（°）は、円を360等分した角度の単位です。
古代メソポタミア文明に由来する、非常に歴史の古い単位で、日常生活や学校の算数でよく使われます。
一方、ラジアンは、より数学的な角度の単位です。
円の中心から円周に伸びる半径の長さと、円周上の弧の長さが等しくなるときの中心角が1ラジアンと定義されます。
この定義から、円一周（360°）の円周の長さは2πr（半径の2π倍）なので、360° = 2πラジアンとなります。
| 度（°） | ラジアン（π基準） | ラジアン（小数） |
|---|---|---|
| 0° | 0 | 0 |
| 30° | π/6 | 0.5235987756 |
| 45° | π/4 | 0.7853981634 |
| 60° | π/3 | 1.0471975512 |
| 90° | π/2 | 1.5707963268 |
| 180° | π | 3.1415926536 |
| 270° | 3π/2 | 4.7123889804 |
| 360° | 2π | 6.2831853072 |
Excelは、引数として入力された数値をすべてラジアンとして解釈するため、90と入力すると90ラジアンの値を計算してしまいます。
90ラジアンは円を14周以上も回った先の角度なので、もちろん0にはなりません。
PI関数とRADIANS関数でラジアンを攻略しよう！
Excelでは、ラジアンへの変換を簡単に行うための関数が用意されています。
- RADIANS(角度)：度数をラジアンに変換する関数
- PI()：円周率π（約3.14159…）の値を返す関数
90°を正確に計算したい場合は、=COS(RADIANS(90))と入力します。
また、πを使って計算したい場合は、=COS(PI()/2)と入力することもできます。
| 計算したい角度 | RADIANS関数を使った数式 | PI関数を使った数式 |
|---|---|---|
| 90° | =COS(RADIANS(90)) | =COS(PI()/2) |
| 180° | =COS(RADIANS(180)) | =COS(PI()) |
| 270° | =COS(RADIANS(270)) | =COS(3*PI()/2) |
| 360° | =COS(RADIANS(360)) | =COS(2*PI()) |
PI()関数を使った方が、数学的な意味がより明確で、計算式が美しいですね！
Excelで三角関数を計算する具体的な手順
ここからは、実際にExcelで三角関数を計算する具体的な例を見ていきましょう。
例1：直角三角形の高さ（対辺）を求める
底辺の長さが10、角度が30°の直角三角形の、高さを求めてみましょう。
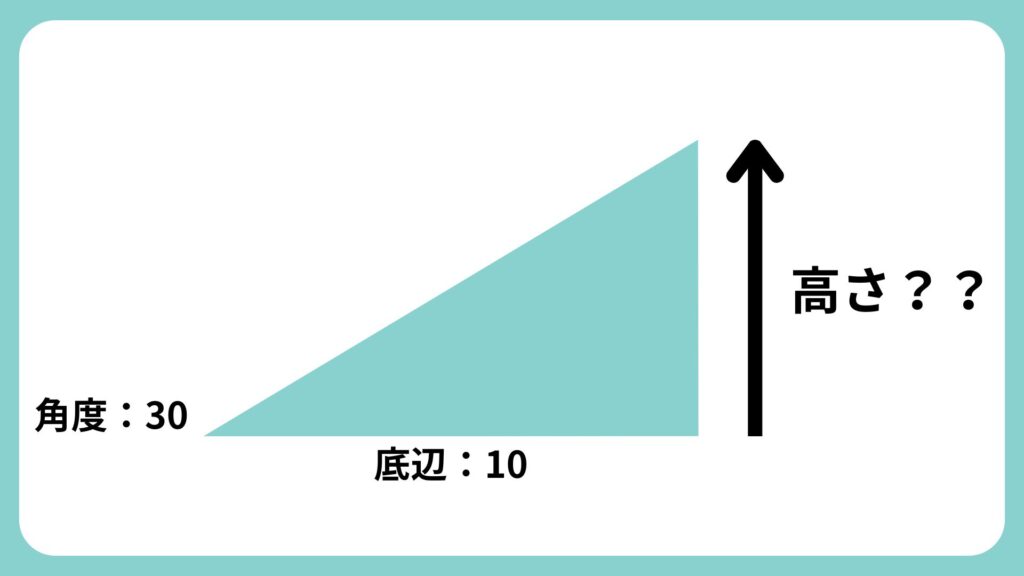
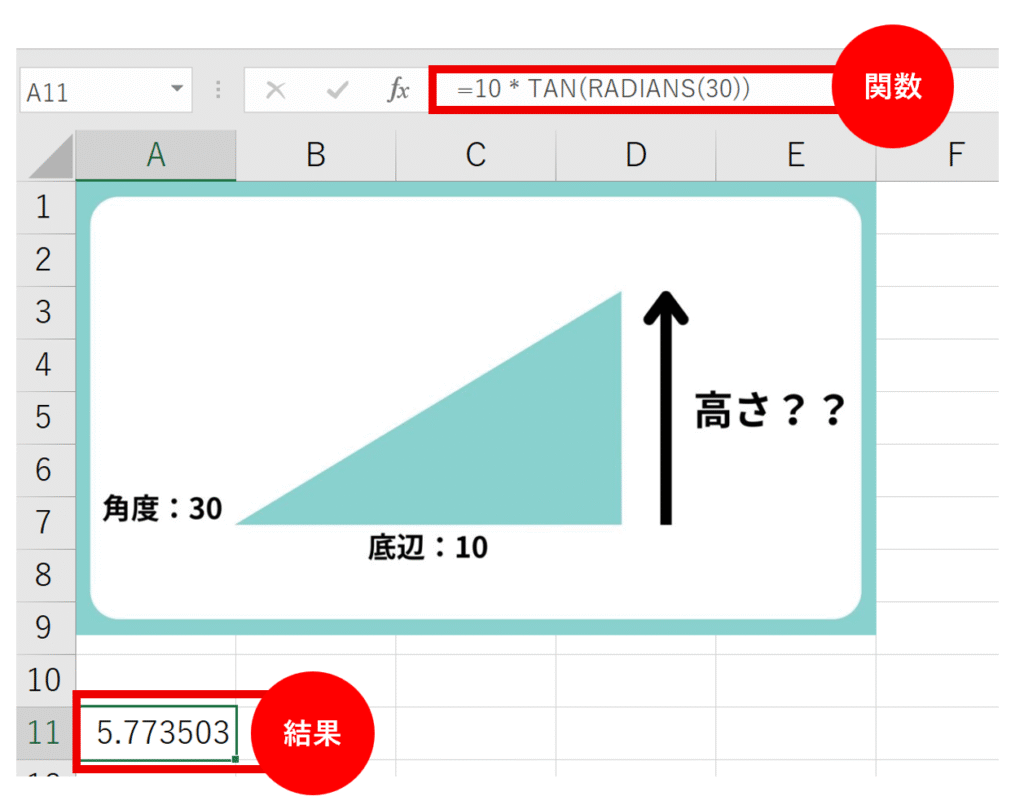
- 使う関数：TAN
- 計算式：高さ = 底辺 × TAN(角度)
数式：
=10 * TAN(RADIANS(30))
または
=10 * TAN(PI()/6)
結果：約5.77
例2：斜辺の長さ（A）を求める
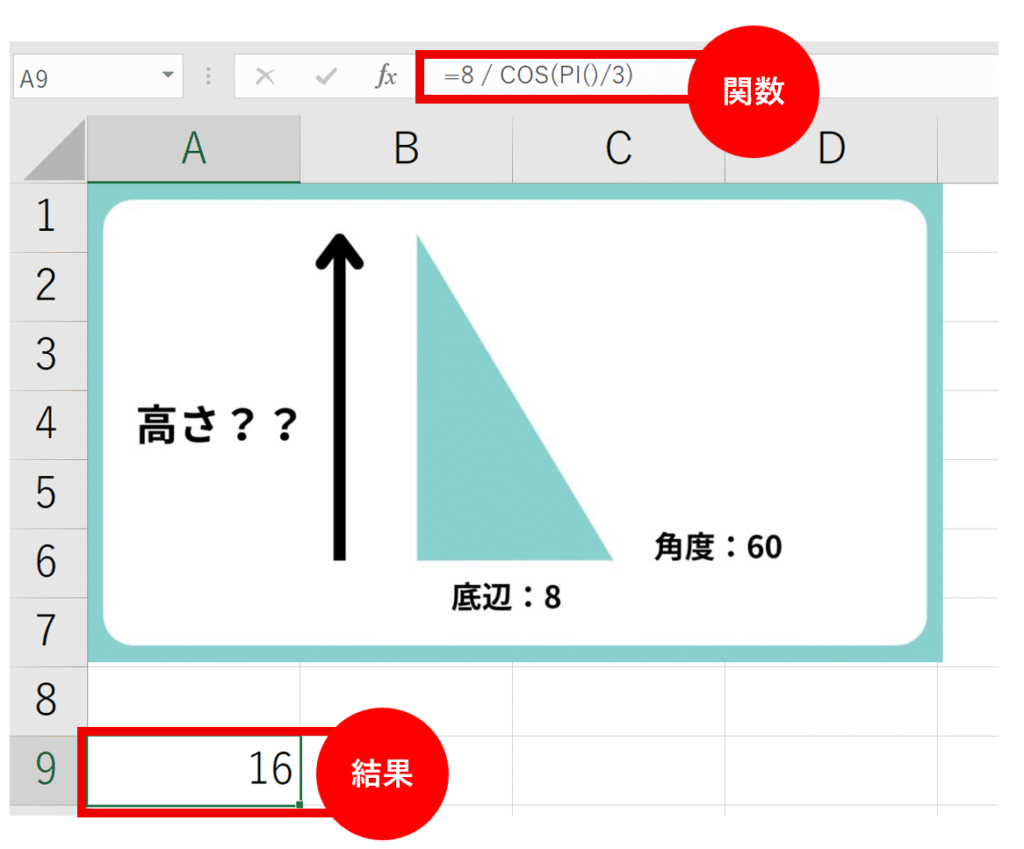
底辺の長さが8、角度が60°の直角三角形の、斜辺の長さを求めてみましょう。
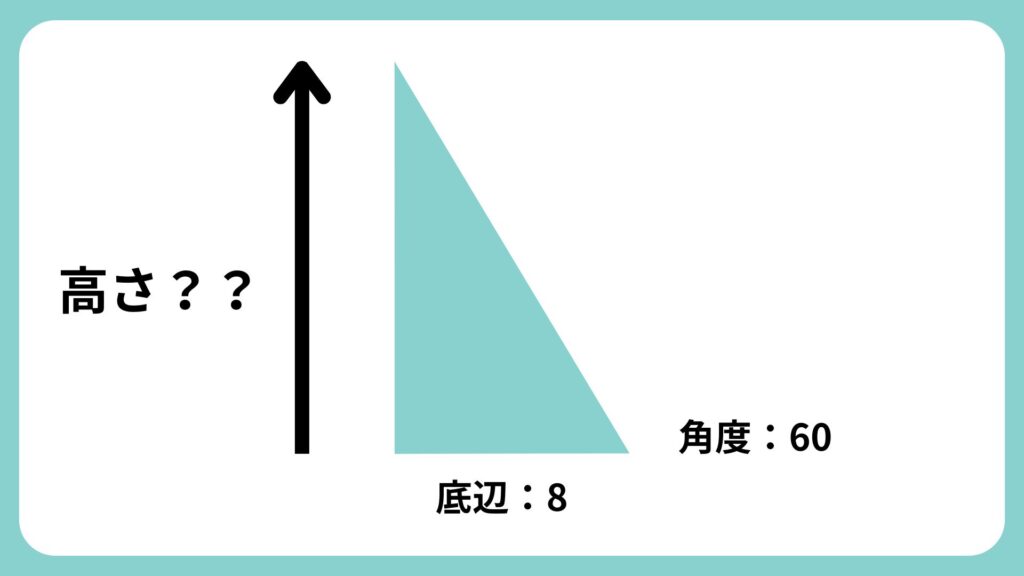
- 使う関数：COS
- 計算式：斜辺 = 底辺 / COS(角度)
数式：
=8 / COS(RADIANS(60))
または
=8 / COS(PI()/3)
結果：16
例3：周期的なグラフを作成する
気温や株価のように周期的な変動をするデータをモデル化する際にも、三角関数は非常に役立ちます。例えば、SIN関数を使って波のようなグラフを作成してみましょう。
- A列に角度を入力：
0から360まで30刻みで角度を入力します。 - B列にラジアンを計算：
B1セルに=RADIANS(A1)と入力し、下にコピーします。 - C列にSINの値を計算：
C1セルに=SIN(B1)と入力し、下にコピーします。 - グラフを作成：
C列を選択し、「挿入」タブから「散布図（平滑線とマーカー）」を選択します。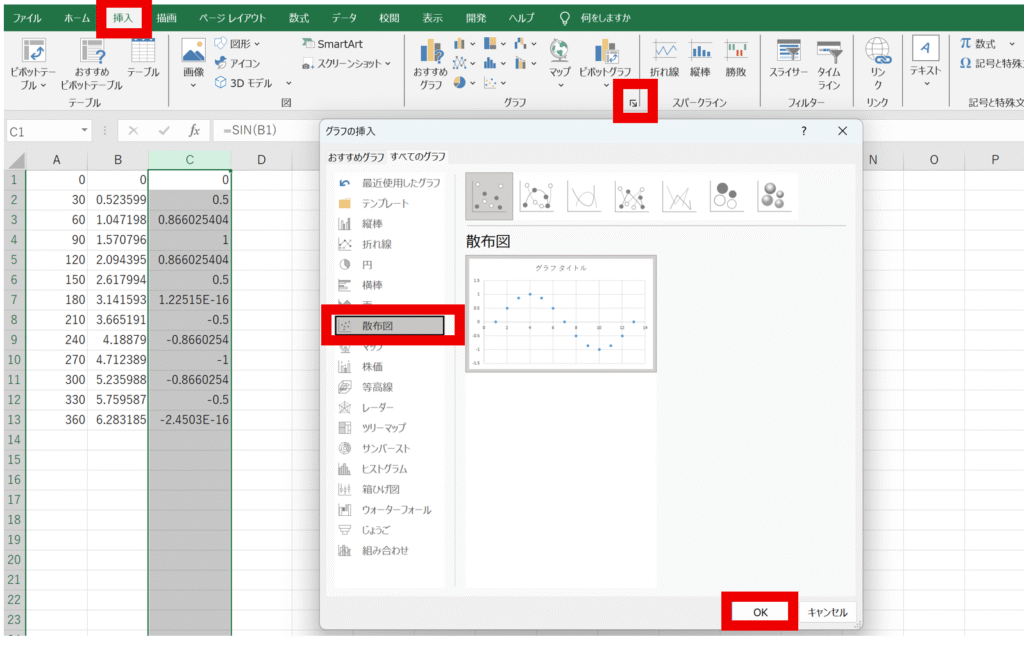
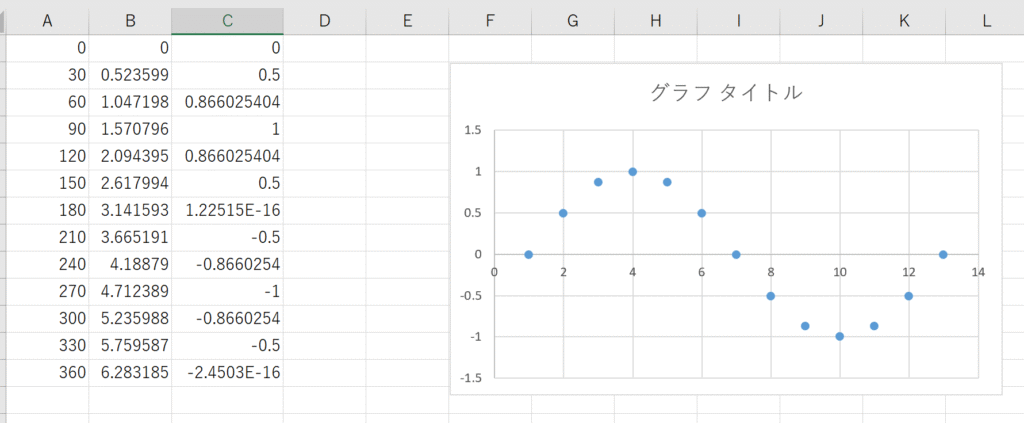
このように、Excelを使えば簡単にグラフ化することも可能です。
例4：ピタゴラスの定理が正しいか確認してみよう
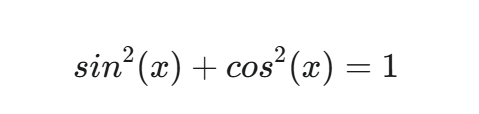
以下の手順で、Excelを使って上記関係式（ピタゴラスの定理）が成立するかを確かめてみましょう。
- 角度の入力:
ExcelのA列に、検証したい角度（度数）をいくつか入力します。例えば、30、45、60、90、180、270といった値をA2セルから下に入力します。 - ラジアンへの変換:
B列に、A列で入力した度数をラジアンに変換する数式を入力します。- B2セルに =RADIANS(A2) と入力し、下にコピーします。
- sin関数の計算:
C列に、ラジアンに変換した角度の sin を計算する数式を入力します。- C2セルに =SIN(B2) と入力し、下にコピーします。
- cos関数の計算:
D列に、ラジアンに変換した角度の cos を計算する数式を入力します。- D2セルに =COS(B2) と入力し、下にコピーします。
- 相互関係の検証:
E列に、sin2(x)+cos2(x) の計算式を入力します。- E2セルに =C2^2 + D2^2 と入力し、下にコピーします。
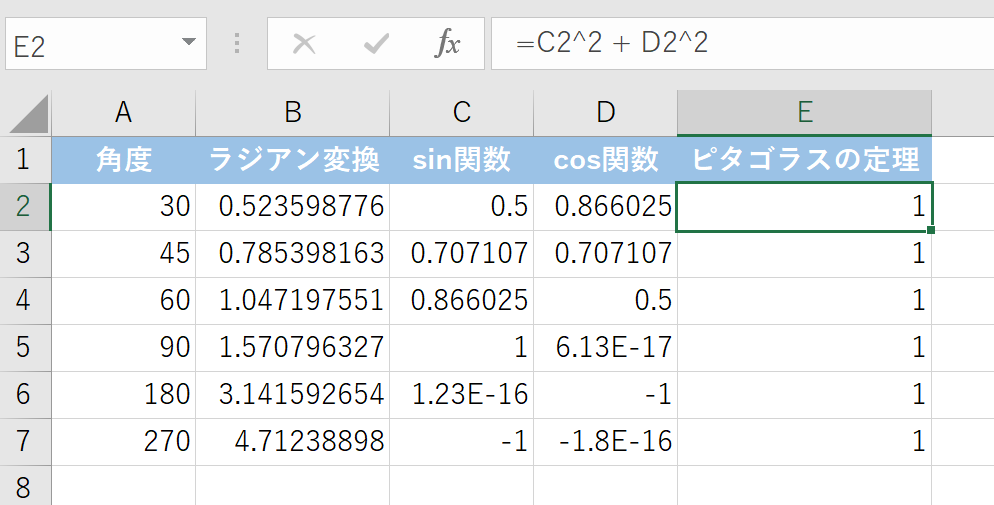
この手順を実行すると、E列のすべてのセルに「1」という値が表示されましたね！
角度を求めたい時は？逆三角関数を使おう！
辺の長さから「角度」を求めたい場合は、逆三角関数を使います。Excelには、それぞれの三角関数に対応する逆関数が用意されています。これらは、頭にA（アーク）が付きます。
| 関数 | 役割 | 出力される単位 |
|---|---|---|
| ASIN | アークサイン（SINの逆） | ラジアン |
| ACOS | アークコサイン（COSの逆） | ラジアン |
| ATAN | アークタンジェント（TANの逆） | ラジアン |
これらの関数は、結果がラジアンで返されます。
私たちが慣れている「度」で表示するには、DEGREES関数を使って変換する必要があります。
逆三角関数の練習問題
ここでは、さらにいくつかの例題を通じて、逆三角関数の使い方をマスターしていきましょう。
問題1：斜辺が10、対辺が5のときの角度は？
- 使う関数：ASIN
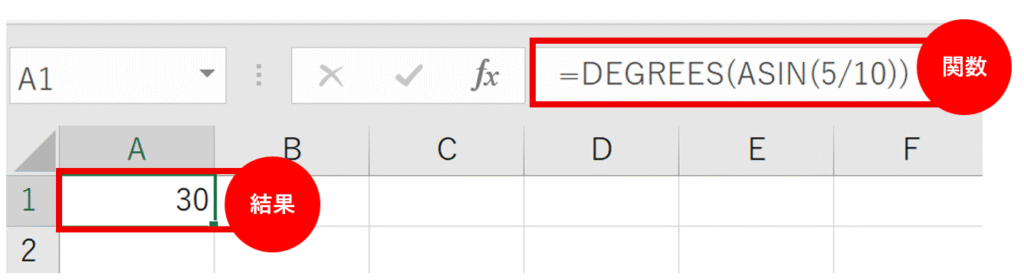
- 数式：=DEGREES(ASIN(5/10))
- 答え：30°
問題2：斜辺が5、底辺が4のときの角度は？
- 使う関数：ACOS
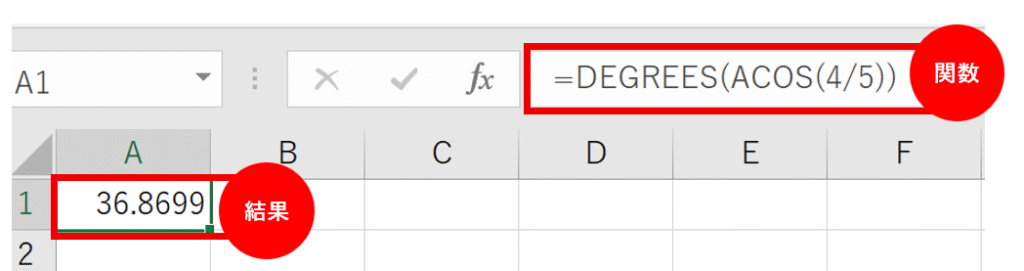
- 数式：=DEGREES(ACOS(4/5))
- 答え：約36.87°
問題3：底辺が8、対辺が6のときの角度は？
- 使う関数：ATAN
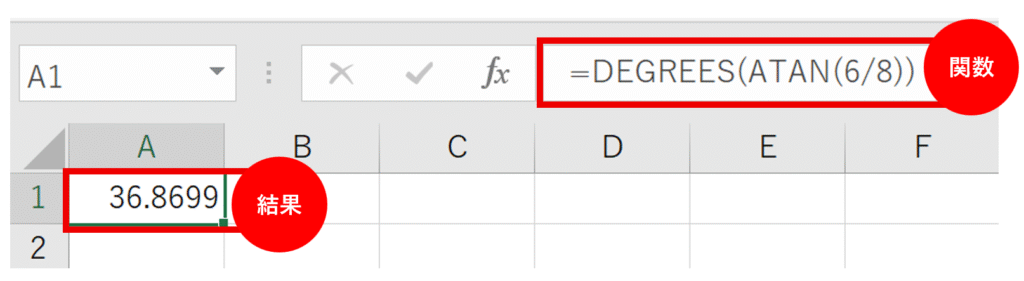
- 数式：=DEGREES(ATAN(6/8))
- 答え：約36.87°
三角関数を使うときの注意点とエラー対処法
- 単位は必ずラジアンに！
- 小数点以下の誤差に注意
- #NUM!エラーが出たら？
注意点1：単位は必ずラジアンに！
最も重要なポイントです。RADIANS関数またはPI()関数を使って、引数をラジアンに変換するのを忘れないようにしましょう。
注意点2：小数点以下の誤差に注意
Excelはコンピューターなので、ごくわずかな計算誤差が発生することがあります。例えば、COS(RADIANS(90))が0ではなく、6.12323E-17のように表示されることがありますが、これはほぼ0と同じです。安心してください。
エラー対処法：#NUM!エラーが出たら？
#NUM!エラーは「無効な数値」を意味します。特にASINやACOSでこのエラーが出た場合は、引数が-1から1の範囲外になっていないか確認してください。SINやCOSは数学的にこの範囲内の値しか取らないため、この範囲外の数値では計算できません。
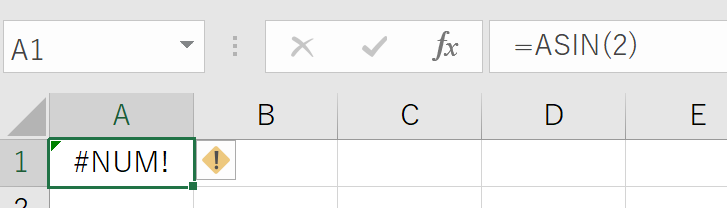
上記のエラー以外にも、=ASIN(1.5)や=ACOS(-1.1)、=ACOS(1.00000000001)でもエラーが出ます。
計算式を見直し、引数が-1と1の間に収まるように修正しましょう。
まとめ
Excelで三角関数を扱うのは、慣れてしまえばとても簡単です。
- Excelの三角関数は「ラジアン」で計算する
- 度数からラジアンへはRADIANS関数かPI()関数を使う
- 角度を求めるときは、ASIN、ACOS、ATANのいずれかを使う
- 逆関数の結果を度数に戻すにはDEGREES関数を使う
これらのポイントを押さえておけば、もうExcelでの三角関数計算で悩むことはありません。ぜひ、今回の内容を参考に、色々な計算に挑戦してみてくださいね！
練習問題
最後に、この記事の内容を試せる練習問題を2つ用意しました。ぜひ、Excelを開いて挑戦してみてください！
問題1: 角度が45°のときのSINとCOSの値を求めてみましょう。
=SIN(RADIANS(45))
⇒ 約0.7071
=COS(RADIANS(45))
⇒ 約0.7071
問題2: 直角三角形の底辺が5、対辺が12のとき、角度は何度になりますか？
=DEGREES(ATAN(12/5))
⇒ 約67.38°
コメント